题目内容
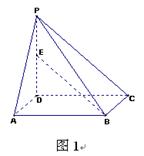
如图,在矩形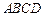 中,
中,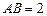 ,
,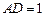 ,
,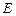 是
是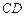 的中点,以
的中点,以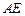 为折
为折 痕将
痕将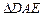 向上折起,使
向上折起,使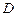 为
为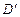 ,且平面
,且平面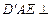 平面
平面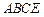
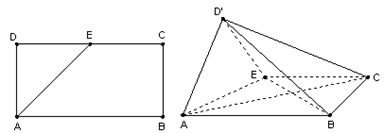
(Ⅰ)求证: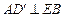 ;
;
(Ⅱ)求二面角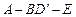 的大小
的大小
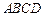 中,
中,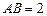 ,
,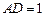 ,
,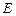 是
是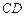 的中点,以
的中点,以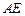 为折
为折 痕将
痕将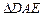 向上折起,使
向上折起,使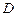 为
为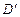 ,且平面
,且平面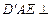 平面
平面

(Ⅰ)求证:
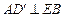 ;
; (Ⅱ)求二面角
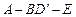 的大小
的大小解:如图所示,
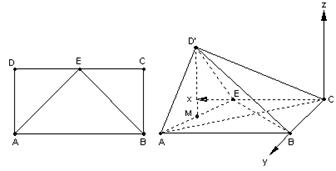
(Ⅰ)证明:因为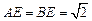 ,
,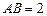 ,所以
,所以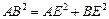 ,即
,即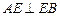 ,…2分
,…2分
取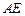 的
的 中点
中点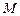 ,连结
,连结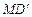 ,则
,则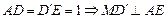 ,
,
又平面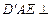 平面
平面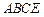 ,可得
,可得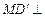 平面
平面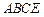 ,即得
,即得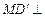
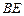 ,…………5分
,…………5分
从而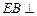 平面
平面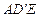 ,故
,故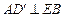 ……………………7分
……………………7分
(Ⅱ)如图建立空间直角坐标系,则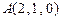 、
、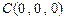 、
、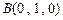 、
、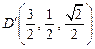 ,
,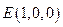 ,从而
,从而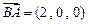 ,
,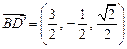 ,
,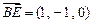 。………9分
。………9分
设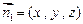 为平面
为平面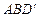 的法向量,
的法向量,
则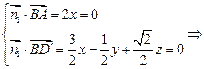 可以取
可以取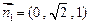 ……………………11分
……………………11分
设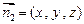 为平面
为平面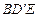 的法向量,
的法向量,
则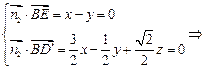 可以取
可以取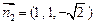 ……………………13分
……………………13分
因此,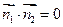 ,有
,有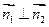 ,即平面
,即平面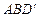
 平面
平面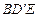 ,
,
故二面角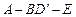 的大小为
的大小为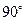 。……………………14分
。……………………14分

(Ⅰ)证明:因为
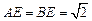 ,
,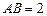 ,所以
,所以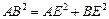 ,即
,即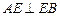 ,…2分
,…2分取
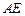 的
的 中点
中点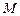 ,连结
,连结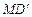 ,则
,则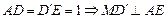 ,
, 又平面
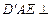 平面
平面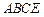 ,可得
,可得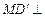 平面
平面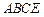 ,即得
,即得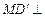
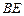 ,…………5分
,…………5分从而
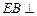 平面
平面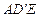 ,故
,故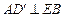 ……………………7分
……………………7分(Ⅱ)如图建立空间直角坐标系,则
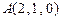 、
、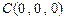 、
、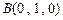 、
、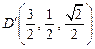 ,
,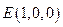 ,从而
,从而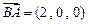 ,
,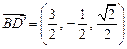 ,
,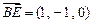 。………9分
。………9分设
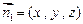 为平面
为平面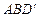 的法向量,
的法向量,则
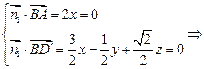 可以取
可以取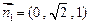 ……………………11分
……………………11分设
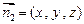 为平面
为平面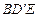 的法向量,
的法向量,则
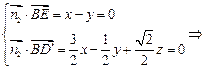 可以取
可以取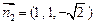 ……………………13分
……………………13分因此,
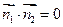 ,有
,有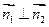 ,即平面
,即平面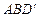
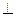 平面
平面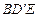 ,
,故二面角
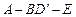 的大小为
的大小为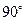 。……………………14分
。……………………14分略

练习册系列答案
相关题目
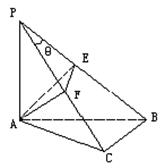
 中
中 ,
, 求证:(1)对角线
求证:(1)对角线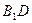 ⊥平面
⊥平面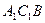 。
。 的外心。
的外心。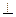 平面ABCD,EC//PD,且PD=2EC。
平面ABCD,EC//PD,且PD=2EC。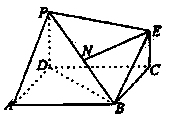
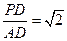 ,求平面PBE与平面ABCD所成的二面角的大小。
,求平面PBE与平面ABCD所成的二面角的大小。 所示的几何体中,
所示的几何体中,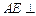 平面
平面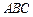 ,
,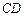 ∥
∥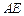 ,
,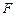 是
是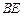 的中点,
的中点,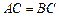
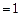 ,
,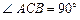 ,
,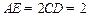 .
.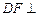 平面
平面 ;
; 的余弦值.
的余弦值.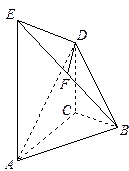
 、
、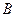 、
、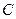 、
、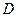 是半径为
是半径为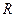 的球面上的四点,且满足
的球面上的四点,且满足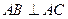 ,
,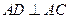 ,
,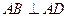 ,则
,则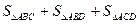 的最大值是 ( )
的最大值是 ( )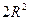
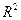
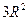
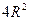
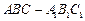 中,
中,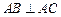 ,顶点
,顶点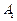 在底面
在底面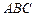 上的射影恰为点B,且
上的射影恰为点B,且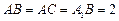 .
.
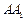 与BC所成的角的大小;
与BC所成的角的大小;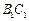 上确定一点P,使
上确定一点P,使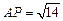 ,并求出二面角
,并求出二面角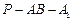 的平面角的余弦值.
的平面角的余弦值.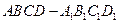 的棱长为2,点
的棱长为2,点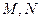 分别为
分别为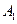
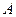 和
和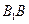 的中点.
的中点.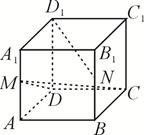
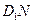 所成角的余弦值;
所成角的余弦值;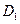 到平面
到平面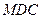 的距离.
的距离.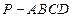 中,底面
中,底面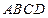 是正方形,
是正方形,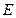 为
为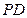 中点,若
中点,若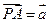 ,
,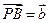 ,
,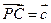 ,
, 则
则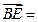 ( )
( )