题目内容
((本小题满分12分)
若图为一简单组合体,其底面ABCD为正方形,PD 平面ABCD,EC//PD,且PD=2EC。
平面ABCD,EC//PD,且PD=2EC。
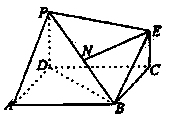
(1)求证:BE//平面PDA;
(2)若N为线段PB的中点,求证:EN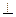 平面PDB;
平面PDB;
(3)若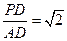 ,求平面PBE与平面ABCD所成的二面角的大小。
,求平面PBE与平面ABCD所成的二面角的大小。
若图为一简单组合体,其底面ABCD为正方形,PD
 平面ABCD,EC//PD,且PD=2EC。
平面ABCD,EC//PD,且PD=2EC。
(1)求证:BE//平面PDA;
(2)若N为线段PB的中点,求证:EN
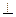 平面PDB;
平面PDB;(3)若
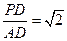 ,求平面PBE与平面ABCD所成的二面角的大小。
,求平面PBE与平面ABCD所成的二面角的大小。(1) 证明:EC∥PD∴EC∥面PAD;同理BC∥面PAD;∴面BEC∥面PAD;∴BE∥面PAD
(2) 证明:取BD的中点O,连NO、CO,易知,CO⊥BD;又∵CO⊥PD; ∴CO⊥面PBD。
(3) 建立如图的空间直角坐标系,令EC=1,则PD=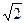
D(0,0,0);P(0,0,2);B(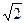 ,
,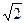 ,0);D(0,
,0);D(0,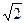 ,1);
,1);
面ABCD的法向量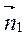 =
=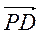 =(0,0,2)
=(0,0,2)
令面PBE的法向量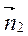 =(x,y,z),则
=(x,y,z),则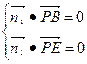 ;则
;则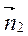 =(1,1,
=(1,1,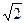 )
)
∴cos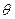 =
=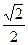 ;∴
;∴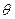 =
=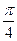
(2) 证明:取BD的中点O,连NO、CO,易知,CO⊥BD;又∵CO⊥PD; ∴CO⊥面PBD。
(3) 建立如图的空间直角坐标系,令EC=1,则PD=
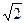
D(0,0,0);P(0,0,2);B(
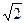 ,
,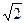 ,0);D(0,
,0);D(0,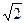 ,1);
,1);面ABCD的法向量
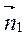 =
=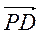 =(0,0,2)
=(0,0,2)令面PBE的法向量
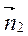 =(x,y,z),则
=(x,y,z),则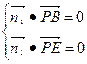 ;则
;则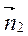 =(1,1,
=(1,1,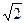 )
)∴cos
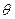 =
=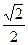 ;∴
;∴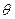 =
=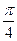
略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
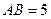 ,AA1=3,点D是AB的中点.
,AA1=3,点D是AB的中点.
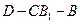 的大小.
的大小.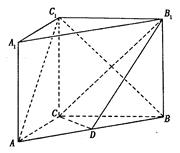
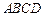 中,
中,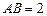 ,
,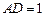 ,
,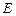 是
是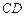 的中点,以
的中点,以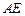 为折
为折 痕将
痕将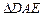 向上折起,使
向上折起,使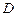 为
为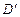 ,且平面
,且平面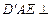 平面
平面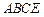
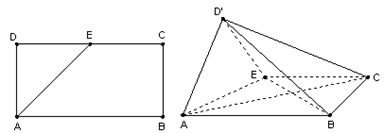
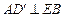 ;
; 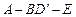 的大小
的大小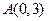 ,
,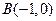 ,
, ,求
,求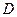 点的坐标,使四边形
点的坐标,使四边形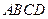 为直角梯形.
为直角梯形. 中,若
中,若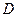 是
是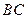 的中点,
的中点,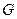 是
是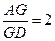 ”.若把该结论推广到空间,则有结论:“在六条棱长都相等
”.若把该结论推广到空间,则有结论:“在六条棱长都相等 的四面体
的四面体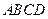 中,若
中,若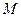 是
是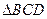 的三边中线的交点,
的三边中线的交点,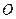 为四面体
为四面体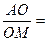 ”
”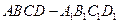 中,直线
中,直线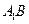 和直线
和直线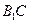 所成的角的大小为( ).
所成的角的大小为( ).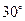
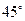


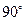
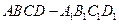 中,
中,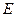 、
、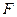 分别是
分别是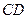 、
、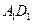 中点
中点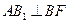 ;
;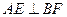 ;
;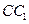 上是否存在点
上是否存在点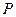 ,使
,使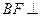 平面
平面 ,若存在,确 定点
,若存在,确 定点