题目内容
已知函数f(x)= .
.
(1)确定y=f(x)在(0,+∞)上的单调性;
(2)若a>0,函数h(x)=xf(x)-x-ax2在(0,2)上有极值,求实数a的取值范围.
 .
.(1)确定y=f(x)在(0,+∞)上的单调性;
(2)若a>0,函数h(x)=xf(x)-x-ax2在(0,2)上有极值,求实数a的取值范围.
(1)在(0,e]上单调递增,在[e,+∞)上单调递减.(2)a>-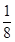 (3)(0,+∞)
(3)(0,+∞)
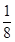 (3)(0,+∞)
(3)(0,+∞)(1)对已知函数f(x)求导得,f′(x)=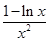 .
.
由1-ln x=0,得x=e.
∴当x∈(0,e)时,f′(x)>0;当x∈(e,+∞)时,f′(x)<0,
∴函数f(x)在(0,e]上单调递增,在[e,+∞)上单调递减.
(2)由h(x)=xf(x)-x-ax2,
可得h(x)=ln x-x-ax2,
则h′(x)=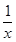 -1-2ax=
-1-2ax=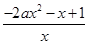 .
.
h(x)=xf(x)-x-ax2在(0,2)上有极值的充要条件是φ(x)=-2ax2-x+1在(0,2)上有零点,
∴φ(0)·φ(2)<0,解得a>-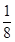 .
.
综上所述,a的取值范围是(0,+∞).
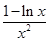 .
.由1-ln x=0,得x=e.
∴当x∈(0,e)时,f′(x)>0;当x∈(e,+∞)时,f′(x)<0,
∴函数f(x)在(0,e]上单调递增,在[e,+∞)上单调递减.
(2)由h(x)=xf(x)-x-ax2,
可得h(x)=ln x-x-ax2,
则h′(x)=
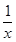 -1-2ax=
-1-2ax=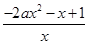 .
.h(x)=xf(x)-x-ax2在(0,2)上有极值的充要条件是φ(x)=-2ax2-x+1在(0,2)上有零点,
∴φ(0)·φ(2)<0,解得a>-
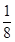 .
.综上所述,a的取值范围是(0,+∞).

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
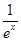 -
-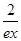 成立.
成立.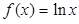 .
.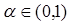 ,求
,求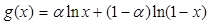 最大值;
最大值;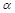 ,
,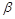 满足
满足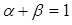 .求证:
.求证: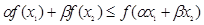 ;
;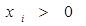 ,正数
,正数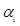 满足
满足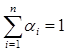 .证明:
.证明: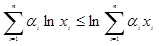
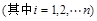 .
.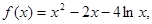 则f′(x)
则f′(x)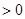 的解集为( )
的解集为( )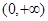
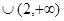
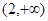
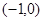
 满足
满足 ,且
,且 为偶函数,当
为偶函数,当 时,有( )
时,有( )



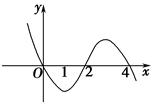
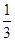 x3-
x3-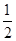 ax2+(a-1)x+1在区间(1,5)上为减函数,在区间(6,+∞)上为增函数,则实数a的取值范围是( )
ax2+(a-1)x+1在区间(1,5)上为减函数,在区间(6,+∞)上为增函数,则实数a的取值范围是( )