题目内容
设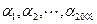 为2008个整数,且
为2008个整数,且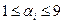 (
(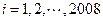 )。如果存在某个
)。如果存在某个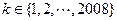 ,使得2008位数
,使得2008位数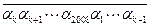 被101整除,试证明:对一切
被101整除,试证明:对一切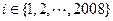 ,2008位数
,2008位数 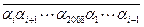 均能被101整除。
均能被101整除。
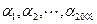 为2008个整数,且
为2008个整数,且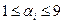 (
(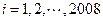 )。如果存在某个
)。如果存在某个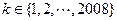 ,使得2008位数
,使得2008位数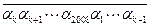 被101整除,试证明:对一切
被101整除,试证明:对一切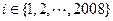 ,2008位数
,2008位数 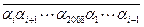 均能被101整除。
均能被101整除。证明略
根据已知条件,不妨设k=1,即2008位数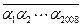 被101整除,只要能证明2008位数
被101整除,只要能证明2008位数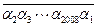 能被101整除。
能被101整除。
事实上,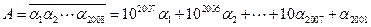 ,
,

从而有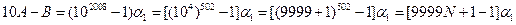 ,
,
即有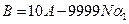 。
。
因为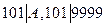 ,所以
,所以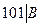 。 利用上述方法依次类推可以得到
。 利用上述方法依次类推可以得到
对一切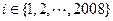 ,2008位数
,2008位数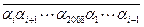 均能被101整除。
均能被101整除。
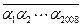 被101整除,只要能证明2008位数
被101整除,只要能证明2008位数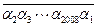 能被101整除。
能被101整除。 事实上,
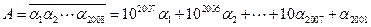 ,
,
从而有
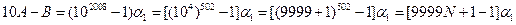 ,
,即有
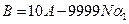 。
。因为
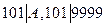 ,所以
,所以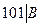 。 利用上述方法依次类推可以得到
。 利用上述方法依次类推可以得到对一切
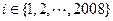 ,2008位数
,2008位数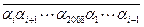 均能被101整除。
均能被101整除。
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
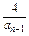 (n≥2),令bn=
(n≥2),令bn=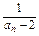 .求证:数列{bn}是等差数列.
.求证:数列{bn}是等差数列.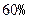 (即衰变了
(即衰变了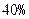 ),该动物大约在距今多少年前死亡?
),该动物大约在距今多少年前死亡?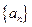 满足,
满足,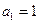 ,
,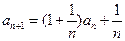 (n∈N*)。
(n∈N*)。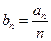 ,求数列
,求数列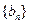 的通项公式;
的通项公式;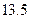 万元的新车,专家预测这种车每年按
万元的新车,专家预测这种车每年按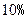 的速度折旧.
的速度折旧.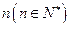 年后这辆车的价值.
年后这辆车的价值. 中,前
中,前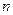 项和为
项和为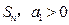 ,且
,且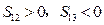 .则
.则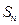 最大?
最大?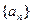 的前
的前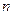 项和为
项和为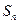 ,且满足
,且满足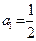 ,
,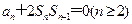 .(1)问:数列
.(1)问:数列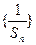 是否为等差数列?并证明你的结论;(2)求
是否为等差数列?并证明你的结论;(2)求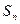 和
和 ;(3)求证:
;(3)求证: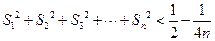 .
.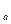 !=(n
!=(n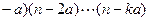 ,其中k是满足n>ka的最大整数,那么
,其中k是满足n>ka的最大整数,那么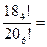 _________
_________