题目内容
1.设函数y=f(x)在R上有定义,对于给定的正数k,定义函数fk(x)=$\left\{\begin{array}{l}{f(x)\\;f(x)≤k}\\{k\\;f(x)>k}\end{array}\right.$,若函数f(x)=$\left\{\begin{array}{l}{{2}^{-x}\\;x≥0}\\{{2}^{x}\\;x<0}\end{array}\right.$,则函数f${\;}_{\frac{1}{2}}$(x)的单调递减区间为( )| A. | (-∞,-1] | B. | (-∞,0] | C. | [0,+∞) | D. | [1,+∞) |
分析 先根据定义,求出函数fk(x)的表达式,然后利用分段函数,确定函数的单调减区间.
解答 解:由定义可知当k=$\frac{1}{2}$时,
f${\;}_{\frac{1}{2}}$(x)=$\left\{\begin{array}{l}{f(x),}&{f(x)≤\frac{1}{2}}\\{\frac{1}{2},}&{f(x)>\frac{1}{2}}\end{array}\right.$,
作出f(x)的图象如图: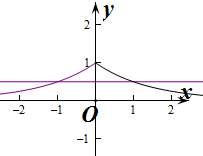
则当x≥0是,由f(x)≤$\frac{1}{2}$得x≥1.由f(x)$>\frac{1}{2}$得0≤x<1,
当x<0是,由f(x)≤$\frac{1}{2}$得x≤-1.由f(x)$>\frac{1}{2}$得-1<x≤0,
即f${\;}_{\frac{1}{2}}$(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x},}&{x≥1}\\{\frac{1}{2},}&{-1<x<1}\\{{2}^{x},}&{x≤-1}\end{array}\right.$,
所以当x≥1时,函数单调递减,即函数fK(x)的单调递减区间为[1,+∞).
故选D.
点评 本题考查了新定义以及指数函数的图象和性质,先利用定义求出函数的表达式,是解决本题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
16.若集合M={x|-2<x<3},N={y|y=lnx+1,x≥1},则集合M∩N等于( )
| A. | (-2,+∞) | B. | (-2,3) | C. | [1,3) | D. | R |