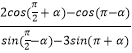题目内容
【题目】五一期间,某商场决定从![]() 种服装、
种服装、![]() 种家电、
种家电、![]() 种日用品中,选出
种日用品中,选出![]() 种商品进行促销活动.
种商品进行促销活动.
(1)试求选出![]() 种商品中至少有一种是家电的概率;
种商品中至少有一种是家电的概率;
(2)商场对选出的某商品采用抽奖方式进行促销,即在该商品现价的基础上将价格提高![]() 元,规定购买该商品的顾客有
元,规定购买该商品的顾客有![]() 次抽奖的机会: 若中一次奖,则获得数额为
次抽奖的机会: 若中一次奖,则获得数额为![]() 元的奖金;若中两次奖,则获得数额为
元的奖金;若中两次奖,则获得数额为![]() 元的奖金;若中三次奖,则共获得数额为
元的奖金;若中三次奖,则共获得数额为 ![]() 元的奖金. 假设顾客每次抽奖中奖的概率都是
元的奖金. 假设顾客每次抽奖中奖的概率都是![]() ,请问: 商场将奖金数额
,请问: 商场将奖金数额![]() 最高定为多少元,才能使促销方案对商场有利?
最高定为多少元,才能使促销方案对商场有利?
【答案】⑴![]() ;⑵
;⑵![]() .
.
【解析】试题分析:
(1)利用题意首先求解没有家电的概率,结合对立事件的概率公式求解至少有一种是家电的概率即可;
(2)利用题意得到关于![]() 的分布列,结合数学期望讨论商场将奖金数额
的分布列,结合数学期望讨论商场将奖金数额![]() 最高定为多少元,才能使促销方案对商场有利即可.
最高定为多少元,才能使促销方案对商场有利即可.
试题解析:
⑴设选出的![]() 种商品中至少有一种是家电为事件A,从
种商品中至少有一种是家电为事件A,从![]() 种服装、
种服装、![]() 种家电、
种家电、![]() 种日用品中,选出
种日用品中,选出![]() 种商品,一共有
种商品,一共有![]() 种不同的选法,
种不同的选法,
选出的![]() 种商品中,没有家电的选法有
种商品中,没有家电的选法有![]() 种,
种,
所以,选出的![]() 种商品中至少有一种是家电的概率为
种商品中至少有一种是家电的概率为![]()
⑵设顾客三次抽奖所获得的奖金总额为随机变量![]() ,其所有可能的取值为0,
,其所有可能的取值为0, ![]() ,
, ![]() ,
, ![]() .(单元:元),
.(单元:元),
![]() 表示顾客在三次抽奖都没有获奖,所以
表示顾客在三次抽奖都没有获奖,所以![]() ,
,
同理![]() ;
;
![]() ;
;
![]() ;
;
顾客在三次抽奖中所获得的奖金总额的期望值是
![]() ,
,
由![]() ,解得
,解得![]() ,
,
所以![]() 最高定为
最高定为![]() 元,才能使促销方案对商场有利.
元,才能使促销方案对商场有利.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目