题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 为何值时,
为何值时,![]() 轴为曲线
轴为曲线![]() 的切线;
的切线;
(2)用![]() 表示
表示![]() 中的最小值,设函数
中的最小值,设函数![]() ,讨论
,讨论![]() 零点的个数.
零点的个数.
【答案】(Ⅰ)![]() ;(Ⅱ)当
;(Ⅱ)当![]() 或
或![]() 时,
时,![]() 由一个零点;当
由一个零点;当![]() 或
或![]() 时,
时,![]() 有两个零点;当
有两个零点;当![]() 时,
时,![]() 有三个零点.
有三个零点.
【解析】试题分析:(Ⅰ)先利用导数的几何意义列出关于切点的方程组,解出切点坐标与对应的![]() 值;(Ⅱ)根据对数函数的图像与性质将
值;(Ⅱ)根据对数函数的图像与性质将![]() 分为
分为![]() 研究
研究![]() 的零点个数,若零点不容易求解,则对
的零点个数,若零点不容易求解,则对![]() 再分类讨论.
再分类讨论.
试题解析:(Ⅰ)设曲线![]() 与
与![]() 轴相切于点
轴相切于点![]() ,则
,则![]() ,
,![]() ,即
,即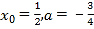 ,解得
,解得![]() .
.
因此,当![]() 时,
时,![]() 轴是曲线
轴是曲线![]() 的切线.
的切线.
(Ⅱ)当![]() 时,
时,![]() ,从而
,从而![]() ,
,
∴![]() 在(1,+∞)无零点.
在(1,+∞)无零点.
当![]() =1时,若
=1时,若![]() ,则
,则![]() ,
,![]() ,故
,故![]() =1是
=1是![]() 的零点;若
的零点;若![]() ,则
,则![]() ,
,![]() ,故
,故![]() =1不是
=1不是![]() 的零点.
的零点.
当![]() 时,
时,![]() ,所以只需考虑
,所以只需考虑![]() 在(0,1)的零点个数.
在(0,1)的零点个数.
(ⅰ)若![]() 或
或![]() ,则
,则![]() 在(0,1)无零点,故
在(0,1)无零点,故![]() 在(0,1)单调,而
在(0,1)单调,而![]() ,
,![]() ,所以当
,所以当![]() 时,
时,![]() 在(0,1)有一个零点;当
在(0,1)有一个零点;当![]() 0时,
0时,![]() 在(0,1)无零点.
在(0,1)无零点.
(ⅱ)若![]() ,则
,则![]() 在(0,
在(0,![]() )单调递减,在(
)单调递减,在(![]() ,1)单调递增,故当
,1)单调递增,故当![]() =
=![]() 时,
时,![]() 取的最小值,最小值为
取的最小值,最小值为![]() =
=![]() .
.
①若![]() >0,即
>0,即![]() <
<![]() <0,
<0,![]() 在(0,1)无零点.
在(0,1)无零点.
②若![]() =0,即
=0,即![]() ,则
,则![]() 在(0,1)有唯一零点;
在(0,1)有唯一零点;
③若![]() <0,即
<0,即![]() ,由于
,由于![]() ,
,![]() ,所以当
,所以当![]() 时,
时,![]() 在(0,1)有两个零点;当
在(0,1)有两个零点;当![]() 时,
时,![]() 在(0,1)有一个零点.…10分
在(0,1)有一个零点.…10分
综上,当![]() 或
或![]() 时,
时,![]() 由一个零点;当
由一个零点;当![]() 或
或![]() 时,
时,![]() 有两个零点;当
有两个零点;当![]() 时,
时,![]() 有三个零点.
有三个零点.

练习册系列答案
相关题目