��Ŀ����
����Ŀ��ij���ճ���ͭ˿5���ף���˿9���ף����������ֲ��ϱ��Ƴɻ����ͻ�����ۣ���֪һֻ������Ҫ��ͭ˿200�ף���˿300�ף�����һֻ������Ҫ100�ף���˿300�ף���ó�������ԭ�����Ƹ�����![]() ��
�� ![]() ������.
������.
�����г�![]() ����Ĺ�ϵʽ����������Ӧ��ƽ������
����Ĺ�ϵʽ����������Ӧ��ƽ������
����������һ�������ɻ���300Ԫ������һ�����̿ɻ���200Ԫ����ô�������Ż����뻨��ı��Ƹ�������ʹ���������������������Ƕ��٣�
���𰸡���1������������2���ó�����200������,100����������������,�������Ϊ8��Ԫ.
�����������������(1)�г�x��y����Ĺ�ϵʽΪ ,��������ʽ������ʾ��ƽ������.
,��������ʽ������ʾ��ƽ������.
(2)��ó���������ΪzԪ,д��Ŀ�꺯��,����Ŀ�꺯���ļ�������,���Ŀ�꺯��z=300x+200y,���������.
���������
(1)����֪x��y����Ĺ�ϵʽΪ �ȼ���
�ȼ���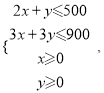
�ö�Ԫһ�β���ʽ������ʾ��ƽ��������ͼ�е���Ӱ����.

(2)��ó���������ΪzԪ,��Ŀ�꺯��Ϊz=300x+200y
��z=300x+200y����Ϊ![]() ,����б��Ϊ
,����б��Ϊ![]() ,��y���Ͻؾ�Ϊ
,��y���Ͻؾ�Ϊ![]() ����z�仯��һ��ƽ��ֱ��.
����z�仯��һ��ƽ��ֱ��.
����Ϊx��y����Լ������,������ͼ��֪,��ֱ��![]() �����������ϵĵ�Mʱ,�ؾ�
�����������ϵĵ�Mʱ,�ؾ�![]() ���,��z���.
���,��z���.
�ⷽ����![]() �õ�M������Ϊ(200,100)��ǡΪ����,��x=200,y=100.
�õ�M������Ϊ(200,100)��ǡΪ����,��x=200,y=100.
����, ![]() .
.
�𣺸ó�����200������,100����������������,�������Ϊ8��Ԫ.

