题目内容
【题目】(题文)如图所示的某种容器的体积为![]() ,它是由圆锥和圆柱两部分连接而成,圆柱与圆锥的底面半径都为
,它是由圆锥和圆柱两部分连接而成,圆柱与圆锥的底面半径都为![]() .圆锥的高为
.圆锥的高为![]() ,母线与底面所成的角为
,母线与底面所成的角为![]() ;圆柱的高为
;圆柱的高为![]() ,已知圆柱底面的造价为
,已知圆柱底面的造价为![]() 元
元![]() ,圆柱侧面造价为
,圆柱侧面造价为![]() 元
元![]() ,圆锥侧面造价为
,圆锥侧面造价为![]()
![]() 元
元![]() .
.
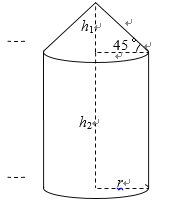
(1)将圆柱的高![]() 表示为底面半径
表示为底面半径![]() 的函数,并求出定义域;
的函数,并求出定义域;
(2)当容器造价最低时,圆柱的底面半径![]() 为多少?
为多少?
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由题意,根据圆锥的体积公式和圆柱的体积公式,即可得到![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)根据圆锥与圆柱的侧面积公式得到容器总造价为![]() ,令
,令![]() ,利用导数求得函数
,利用导数求得函数![]() 的单调性,即可得到函数
的单调性,即可得到函数![]() 最小值,得到解答.
最小值,得到解答.
(1)解:因为圆锥的母线与底面所成的角为![]() ,所以
,所以![]() ,
,
圆锥的体积为![]() ,圆柱的体积为
,圆柱的体积为![]() .
.
因为![]() ,所以
,所以![]() ,
,
所以![]() .
.
因为![]() ,所以
,所以![]() .因此
.因此![]() .
.
所以![]() ,定义域为
,定义域为![]() .
.
(2)圆锥的侧面积![]() ,
,
圆柱的侧面积![]() ,底面积
,底面积![]() .
.
容器总造价为![]()
![]()
![]()
![]()
![]() .
.
令![]() ,则
,则![]() .令
.令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为单调减函数;
上为单调减函数;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为单调增函数.
上为单调增函数.
因此,当且仅当![]() 时,
时,![]() 有最小值,y有最小值90
有最小值,y有最小值90![]() 元.
元.
所以,总造价最低时,圆柱底面的半径为3cm.

【题目】深受广大球迷喜爱的某支欧洲足球队.在对球员的使用上总是进行数据分析,为了考察甲球员对球队的贡献,现作如下数据统计:
球队胜 | 球队负 | 总计 | |
甲参加 |
|
|
|
甲未参加 |
|
|
|
总计 |
|
|
|
(1)求![]() 的值,据此能否有
的值,据此能否有![]() 的把握认为球队胜利与甲球员参赛有关;
的把握认为球队胜利与甲球员参赛有关;
(2)根据以往的数据统计,乙球员能够胜任前锋、中锋、后卫以及守门员四个位置,且出场率分别为:![]() ,当出任前锋、中锋、后卫以及守门员时,球队输球的概率依次为:
,当出任前锋、中锋、后卫以及守门员时,球队输球的概率依次为:![]() .则:
.则:
1)当他参加比赛时,求球队某场比赛输球的概率;
2)当他参加比赛时,在球队输了某场比赛的条件下,求乙球员担当前锋的概率;
3)如果你是教练员,应用概率统计有关知识.该如何使用乙球员?
附表及公式:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() .
.
【题目】为了鼓励节约用电,辽宁省实行阶梯电价制度,其中每户的用电单价与户年用电量的关系如下表所示.
分档 | 户年用电量(度) | 用电单价(元/度) |
第一阶梯 |
| 0.5 |
第二阶梯 |
| 0.55 |
第三阶梯 |
| 0.80 |
记用户年用电量为![]() 度时应缴纳的电费为
度时应缴纳的电费为![]() 元.
元.
(1)写出![]() 的解析式;
的解析式;
(2)假设居住在沈阳的范伟一家2018年共用电3000度,则范伟一家2018年应缴纳电费多少元?
(3)居住在大连的张莉一家在2018年共缴纳电费1942元,则张莉一家在2018年用了多少度电?


