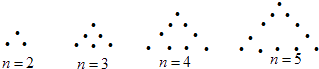ЬтФПФкШн
ЁОЬтФПЁПФГЭцОпЩњВњЙЋЫОУПЬьМЦЛЎЩњВњЮРБјЁЂЦяБјЁЂЩЁБјетШ§жжЭцОпЙВ![]() ИіЃЌЩњВњвЛИіЮРБјаш
ИіЃЌЩњВњвЛИіЮРБјаш![]() ЗжжгЃЌЩњВњвЛИіЦяБјаш
ЗжжгЃЌЩњВњвЛИіЦяБјаш![]() ЗжжгЃЌЩњВњвЛИіЩЁБјаш
ЗжжгЃЌЩњВњвЛИіЩЁБјаш![]() ЗжжгЃЌвбжЊзмЩњВњЪБМфВЛГЌЙ§
ЗжжгЃЌвбжЊзмЩњВњЪБМфВЛГЌЙ§![]() аЁЪБЃЌШєЩњВњвЛИіЮРБјПЩЛёРћШѓ
аЁЪБЃЌШєЩњВњвЛИіЮРБјПЩЛёРћШѓ![]() дЊЃЌЩњВњвЛИіЦяБјПЩЛёРћШѓ
дЊЃЌЩњВњвЛИіЦяБјПЩЛёРћШѓ![]() дЊЃЌЩњВњвЛИіЩЁБјПЩЛёРћШѓ
дЊЃЌЩњВњвЛИіЩЁБјПЩЛёРћШѓ![]() дЊ.
дЊ.
ЃЈ1ЃЉгУУПЬьЩњВњЕФЮРБјИіЪ§![]() гыЦяБјИіЪ§
гыЦяБјИіЪ§![]() БэЪОУПЬьЕФРћШѓ
БэЪОУПЬьЕФРћШѓ![]() ЃЈдЊЃЉЃЛ
ЃЈдЊЃЉЃЛ
ЃЈ2ЃЉдѕУДЗжХфЩњВњШЮЮёВХФмЪЙУПЬьЕФРћШѓзюДѓЃЌзюДѓРћШѓЪЧЖрЩйЃП

ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉУПЬьЩњВњЕФЮРБјИіЪ§ЮЊ
ЃЛЃЈ2ЃЉУПЬьЩњВњЕФЮРБјИіЪ§ЮЊ![]() ЃЌЦяБјИіЪ§ЮЊ
ЃЌЦяБјИіЪ§ЮЊ![]() ЃЌЩЁБјИіЪ§ЮЊ
ЃЌЩЁБјИіЪ§ЮЊ![]() ЪБРћШѓзюДѓЃЌзюДѓРћШѓЮЊ
ЪБРћШѓзюДѓЃЌзюДѓРћШѓЮЊ![]() дЊ..
дЊ..
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЯШаДГіУПЬьЩњВњЕФЩЁБјИіЪ§ЃЌСаГіРћШѓwЙигкxЕФКЏЪ§;
ЃЈ2ЃЉгЩдМЪјЬѕМўећРэКѓЛГіПЩаагђЃЌаДГіФПБъКЏЪ§ЃЌЭЈЙ§жБЯпЦНвЦСюw=0ЕФжБЯпЃЌПЩОЙ§ЕуAЪБЃЌwгазюДѓжЕЃЎЧѓГіЕуAЕФзјБъЃЌДгЖјЧѓЕУЛёЕУзюДѓЮЊРћШѓЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉвРЬтвтУПЬьЩњВњЕФЩЁБјИіЪ§ЮЊ100ЃxЃyЃЌ
ЫљвдРћШѓwЃН5xЃЋ6yЃЋ3ЃЈ100ЃxЃyЃЉЃН2xЃЋ3yЃЋ300.
ЃЈ2ЃЉдМЪјЬѕМўЮЊ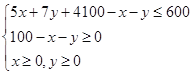
ећРэЕУ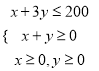
ФПБъКЏЪ§ЮЊwЃН2xЃЋ3yЃЋ300.
зїГіПЩаагђЃЎШчЭМЫљЪОЃК
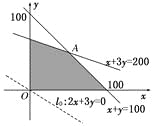
ГѕЪМжБЯпl0ЃК2xЃЋ3yЃН0ЃЌЦНвЦГѕЪМжБЯпОЙ§ЕуAЪБЃЌwгазюДѓжЕЃЎ
гЩ![]() ЕУ
ЕУ![]()
зюгХНтЮЊAЃЈ50,50ЃЉЃЌЫљвдwmaxЃН550дЊЃЎ
ЫљвдУПЬьЩњВњЮРБј50ИіЃЌЦяБј50ИіЃЌЩЁБј0ИіЪБРћШѓзюЃЌзюДѓЮЊРћШѓ550дЊЃЎ

 ЦкФЉКУГЩМЈЯЕСаД№АИ
ЦкФЉКУГЩМЈЯЕСаД№АИ 99Мг1СьЯШЦкФЉЬибЕОэЯЕСаД№АИ
99Мг1СьЯШЦкФЉЬибЕОэЯЕСаД№АИ АйЧПУћаЃЦкФЉГхДЬ100ЗжЯЕСаД№АИ
АйЧПУћаЃЦкФЉГхДЬ100ЗжЯЕСаД№АИ КУГЩМЈ1Мг1ЦкФЉГхДЬ100ЗжЯЕСаД№АИ
КУГЩМЈ1Мг1ЦкФЉГхДЬ100ЗжЯЕСаД№АИ Н№зДдЊМЈгХКУОэЯЕСаД№АИ
Н№зДдЊМЈгХКУОэЯЕСаД№АИ