题目内容
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,右顶点为
,右顶点为![]() ,点
,点![]() 的坐标为
的坐标为![]() 的面积为
的面积为![]() ,过点
,过点![]() 的动直线
的动直线![]() 被椭圆
被椭圆![]() 所截得的线段
所截得的线段![]() 长度的最小值为
长度的最小值为![]() .
.
(I)求椭圆![]() 的方程;
的方程;
(Ⅱ) ![]() 是椭圆
是椭圆![]() 上异于顶点的一点,且直线
上异于顶点的一点,且直线![]() 是线段
是线段![]() 延长线上一点,且
延长线上一点,且![]() ,
,![]() 的半径为
的半径为![]() 是
是![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,求
,求![]() 的最大值,并求出取得最大值时直线
的最大值,并求出取得最大值时直线![]() 的斜率 .
的斜率 .
【答案】(Ⅰ) ![]() (Ⅱ)
(Ⅱ)![]() 的最大值为
的最大值为![]() ,取得最大值时直线
,取得最大值时直线![]() 的斜率为
的斜率为![]() .
.
【解析】分析:(Ⅰ)由已知,可得![]() ,解得
,解得![]() 设椭圆
设椭圆![]() 方程:
方程:![]() ,
,
当直线![]() 斜率不存在时,线段
斜率不存在时,线段![]() 长为
长为![]() ;
;
当直线![]() 斜率存在时,设
斜率存在时,设![]() 方程:
方程:![]() ,由弦长公式可得
,由弦长公式可得![]() 的长小于
的长小于![]() ,
,
易知当![]() 时,
时,![]() 的最小值为
的最小值为![]() ,从而
,从而![]() ,由此得到椭圆
,由此得到椭圆![]() 的方程;(
的方程;(
Ⅱ)由(Ⅰ)知,![]() ,而
,而![]() 的半径
的半径![]() ,
,
又直线![]() 的方程为
的方程为![]() ,可得
,可得 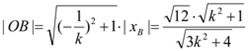 ,
,
由题意可知![]() ,要求
,要求![]() 的最大值,即求
的最大值,即求![]() 的最小值,由题意可知
的最小值,由题意可知![]() ,转化为关于
,转化为关于![]() 的函数,换元后利用配方法可得
的函数,换元后利用配方法可得
![]() 的最大值,以及取得最大值时直线
的最大值,以及取得最大值时直线![]() 的斜率 .
的斜率 .
详解:
(Ⅰ)由已知,可得![]() .又由
.又由![]() ,可得
,可得![]() ,解得
,解得![]()
设椭圆![]() 方程:
方程:![]() ,
,
当直线![]() 斜率不存在时,线段
斜率不存在时,线段![]() 长为
长为![]() ;
;
当直线![]() 斜率存在时,设
斜率存在时,设![]() 方程:
方程:![]() ,
,
由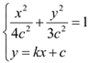 ,得
,得![]() ,从而
,从而
![]()
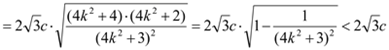 ,
,
易知当![]() 时,
时,![]() 的最小值为
的最小值为![]() ,从而
,从而![]() ,因此,椭圆
,因此,椭圆![]() 的方程为:
的方程为:![]() .
.
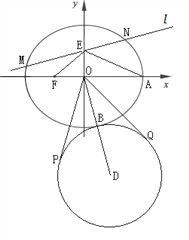
(Ⅱ)由第(Ⅰ)问知,![]() ,而
,而![]() 的半径
的半径![]() ,
,
又直线![]() 的方程为
的方程为![]() ,由
,由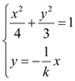 ,得
,得![]() ,
,
因此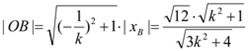 ,
,
由题意可知![]() ,要求
,要求![]() 的最大值,即求
的最大值,即求![]() 的最小值
的最小值
而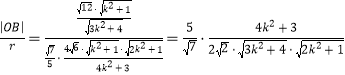
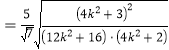 ,令
,令![]() ,则
,则![]() ,
,
因此,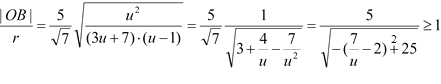 ,
,
当且仅当![]() ,即
,即![]() 时等号成立,此时
时等号成立,此时![]() ,
,
所以![]() ,因此
,因此![]() ,所以
,所以![]() 的最大值为
的最大值为![]() .
.
综上所述,![]() 的最大值为
的最大值为![]() ,取得最大值时直线
,取得最大值时直线![]() 的斜率为
的斜率为![]() .
.

【题目】某建材商场国庆期间搞促销活动,规定:顾客购物总金额不超过800元,不享受任何折扣;如果顾客购物总金额超过800元,则超过800元部分享受一定的折扣优惠,并按下表折扣分别累计计算:
可以享受折扣优惠金额 | 折扣率 |
不超过500元的部分 |
|
超过500元的部分 |
|
若某顾客在此商场获得的折扣金额为50元,则此人购物实际所付金额为![]()
![]()
A.1500元B.1550元C.1750元D.1800元
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 5 |
| 0 |
(1)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数![]() 的解析式;
的解析式;
(2)将![]() 图象上所有点向左平行移动
图象上所有点向左平行移动![]() 个单位长度,并把图象上所有点的横坐标缩短为原来的
个单位长度,并把图象上所有点的横坐标缩短为原来的![]() (纵坐标不变),得到
(纵坐标不变),得到![]() 的图象.若
的图象.若![]() 图象的一个对称中心为
图象的一个对称中心为![]() ,求
,求![]() 的最小值;
的最小值;
(3)在(2)条件下,求![]() 在
在![]() 上的增区间.
上的增区间.