题目内容
【题目】设椭圆 ![]() +
+ ![]() =1(a>b>0)的左焦点为F,右顶点为A,离心率为
=1(a>b>0)的左焦点为F,右顶点为A,离心率为 ![]() .已知A是抛物线y2=2px(p>0)的焦点,F到抛物线的准线l的距离为
.已知A是抛物线y2=2px(p>0)的焦点,F到抛物线的准线l的距离为 ![]() .
.
(Ⅰ)求椭圆的方程和抛物线的方程;
(Ⅱ)设l上两点P,Q关于x轴对称,直线AP与椭圆相交于点B(B异于A),直线BQ与x轴相交于点D.若△APD的面积为 ![]() ,求直线AP的方程.
,求直线AP的方程.
【答案】(Ⅰ)解:设F的坐标为(﹣c,0).
依题意可得  ,
,
解得a=1,c= ![]() ,p=2,于是b2=a2﹣c2=
,p=2,于是b2=a2﹣c2= ![]() .
.
所以,椭圆的方程为x2+ ![]() =1,抛物线的方程为y2=4x.
=1,抛物线的方程为y2=4x.
(Ⅱ)解:直线l的方程为x=﹣1,设直线AP的方程为x=my+1(m≠0),
联立方程组 ![]() ,解得点P(﹣1,﹣
,解得点P(﹣1,﹣ ![]() ),故Q(﹣1,
),故Q(﹣1, ![]() ).
).
联立方程组 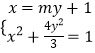 ,消去x,整理得(3m2+4)y2+6my=0,解得y=0,或y=﹣
,消去x,整理得(3m2+4)y2+6my=0,解得y=0,或y=﹣ ![]() .
.
∴B( ![]() ,
, ![]() ).
).
∴直线BQ的方程为( ![]() ﹣
﹣ ![]() )(x+1)﹣(
)(x+1)﹣( ![]() )(y﹣
)(y﹣ ![]() )=0,
)=0,
令y=0,解得x= ![]() ,故D(
,故D( ![]() ,0).
,0).
∴|AD|=1﹣ ![]() =
= ![]() .
.
又∵△APD的面积为 ![]() ,∴
,∴ ![]() ×
× ![]() =
= ![]() ,
,
整理得3m2﹣2 ![]() |m|+2=0,解得|m|=
|m|+2=0,解得|m|= ![]() ,∴m=±
,∴m=± ![]() .
.
∴直线AP的方程为3x+ ![]() y﹣3=0,或3x﹣
y﹣3=0,或3x﹣ ![]() y﹣3=0.
y﹣3=0.
【解析】(Ⅰ)根据椭圆和抛物线的定义、性质列方程组求出a,b,p即可得出方程;(Ⅱ)设AP方程为x=my+1,联立方程组得出B,P,Q三点坐标,从而得出直线BQ的方程,解出D点坐标,根据三角形的面积列方程解出m即可得出答案.
【考点精析】根据题目的已知条件,利用椭圆的标准方程的相关知识可以得到问题的答案,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目