题目内容
【题目】定义在（﹣1，1）上的函数f（x）满足：f（x）﹣f（y）=f（ 
），当x∈（﹣1，0）时，有f（x）＞0；若P=f（ 
）+f（ 
），Q=f（ 
），R=f（0）；则P，Q，R的大小关系为 ．
【答案】R＞P＞Q
【解析】解：∵定义在（﹣1，1）上的函数f（x）满足：f（x）﹣f（y）=f（ 
），∴令x=y，则f（x）﹣f（x）=f（0），即f（0）=0，
令x=0，则f（0）﹣f（y）=f（﹣y），即f（﹣y）=﹣f（y），
∴f（x）在（﹣1，1）是奇函数，
∵当x∈（﹣1，0）时，有f（x）＞0，
∴当x∈（0，1）时，有f（x）＜0．
令x= 
，y= 
，则f（ ）﹣f（ ）=f（ 
）=f（ 
），
∴f（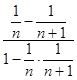 
）+f（ 
）=f（ 
）﹣f（ 
）+f（ ）﹣f（ 
）=f（ ）﹣f（ ），
∴P﹣Q=﹣f（ ）＞0，P＞Q，
∵P，Q＜0，
∴R＞P＞Q．
所以答案是：R＞P＞Q．
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
【题目】近年来我国电子商务行业迎来发展的新机遇，2016年双11期间,某购物平台的销售业
绩高达1207亿人民币。与此同时，相关管理部门推出了针对电商的商品和服务的评价体系，现从评价系统中选出200次成功交易，并对其评价进行统计，对商品的好评率为0.9，对服务的好评率为0.75，其中对商品和服务都做出好评的交易为140次.
(1)请完成下表，并判断是否可以在犯错误概率不超过0.5%的前提下，认为商品好评与服务好评有关？
(2)若将频率视为概率,某人在该购物平台上进行的3次购物中,设对商品和服务全好评的次数为随机变量
：
①求对商品和服务全好评的次数
的分布列；
②求
的数学期望和方差.
（
,其中
）
对服务好评 | 对服务不满意 | 合计 | |
对商品好评 | 140 | ||
对商品不满意 | 10 | ||
合计 | 200 |
