题目内容
【题目】已知二次函数f(x)满足f(x+1)﹣f(x)=﹣2x+1且f(2)=15.
(1)求函数f(x)的解析式;
(2)令g(x)=(2﹣2m)x﹣f(x);
①若函数g(x)在x∈[0,2]上是单调函数,求实数m的取值范围;
②求函数g(x)在x∈[0,2]的最小值.
【答案】
(1)解:设f(x)=ax2+bx+c,
∵f(2)=15,f(x+1)﹣f(x)=﹣2x+1,
∴4a+2b+c=15;a(x+1)2+b(x+1)+c﹣(ax2+bx+c)=﹣2x+1;
∴2a=﹣2,a+b=1,4a+2b+c=15,解得a=﹣1,b=2,c=15,
∴函数f(x)的表达式为f(x)=﹣x2+2x+15
(2)解:∵g(x)=(2﹣2m)x﹣f(x)=x2﹣2mx﹣15的图象是开口朝上,且以x=m为对称轴的抛物线,
①若函数g(x)在x∈[0,2]上是单调函数,则m≤0,或m≥2;
②当m≤0时,g(x)在[0,2]上为增函数,当x=0时,函数g(x)取最小值﹣15;
当0<m<2时,g(x)在[0,m]上为减函数,在[m,2]上为增函数,当x=m时,函数g(x)取最小值﹣m2﹣15;
当m≥2时,g(x)在[0,2]上为减函数,当x=2时,函数g(x)取最小值﹣4m﹣11;
∴函数g(x)在x∈[0,2]的最小值为 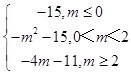
【解析】(1)据二次函数的形式设出f(x)的解析式,将已知条件代入,列出方程,令方程两边的对应系数相等解得.(2)函数g(x)的图象是开口朝上,且以x=m为对称轴的抛物线,①若函数g(x)在x∈[0,2]上是单调函数,则m≤0,或m≥2;②分当m≤0时,当0<m<2时,当m≥2时三种情况分别求出函数的最小值,可得答案.
【考点精析】通过灵活运用二次函数的性质,掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减即可以解答此题.
上递减即可以解答此题.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案【题目】近年来我国电子商务行业迎来发展的新机遇,2016年双11期间,某购物平台的销售业
绩高达1207亿人民币。与此同时,相关管理部门推出了针对电商的商品和服务的评价体系,现从评价系统中选出200次成功交易,并对其评价进行统计,对商品的好评率为0.9,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为140次.
(1)请完成下表,并判断是否可以在犯错误概率不超过0.5%的前提下,认为商品好评与服务好评有关?
(2)若将频率视为概率,某人在该购物平台上进行的3次购物中,设对商品和服务全好评的次数为随机变量![]() :
:
①求对商品和服务全好评的次数![]() 的分布列;
的分布列;
②求![]() 的数学期望和方差.
的数学期望和方差.

( ,其中
,其中![]() )
)
对服务好评 | 对服务不满意 | 合计 | |
对商品好评 | 140 | ||
对商品不满意 | 10 | ||
合计 | 200 |