题目内容
【题目】已知f(x)是定义在R上的奇函数.当x>0时,f(x)=x2﹣4x,则不等式f(x)<x的解集用区间表示为 .
【答案】(﹣∞,﹣5)∪(0,5)
【解析】解:作出f(x)=x2﹣4x(x>0)的图象,如图所示,∵f(x)是定义在R上的奇函数,
∴利用奇函数图象关于原点对称作出x<0的图象,
不等式f(x)<x表示函数y=f(x)图象在y=x下方,
∵f(x)图象与y=x图象交于P(5,5),Q(﹣5,﹣5),
则由图象可得不等式f(x)<x的解集为(﹣∞,﹣5)∪(0,5)
故答案为:(﹣∞,﹣5)∪(0,5)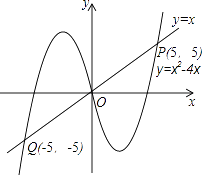
作出x大于0时,f(x)的图象,根据f(x)为定义在R上的奇函数,利用奇函数的图象关于原点对称作出x小于0的图象,所求不等式即为函数y=f(x)图象在y=x下方,利用图形即可求出解集.

练习册系列答案
相关题目