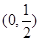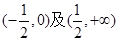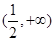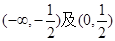题目内容
(本题满分12分)
已知函数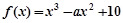 ,
,
(Ⅰ)当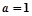 时,求函数
时,求函数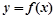 的单调递增区间;
的单调递增区间;
(Ⅱ)在区间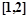 内至少存在一个实数
内至少存在一个实数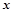 ,使得
,使得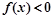 成立,求实数
成立,求实数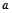 的取值范围.
的取值范围.
已知函数
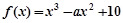 ,
,(Ⅰ)当
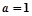 时,求函数
时,求函数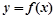 的单调递增区间;
的单调递增区间;(Ⅱ)在区间
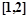 内至少存在一个实数
内至少存在一个实数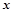 ,使得
,使得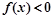 成立,求实数
成立,求实数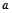 的取值范围.
的取值范围.(I)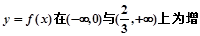 ;(II)
;(II)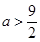 .
.
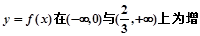 ;(II)
;(II)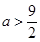 .
. (I)直接求出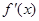 ,然后利用
,然后利用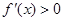 解出f(x)的单调递增区间.
解出f(x)的单调递增区间.
(II)本小题的实质是求f(x)在[1,2]的最小值,根据f(x)的最小值小于零求a的取值范围.在求f(x)的最小值时,要利用导数解决.
(I)当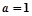 时,
时,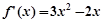
当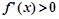 得
得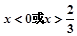
所以函数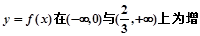
(II)解1: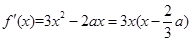
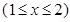
当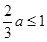 ,即
,即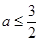 时,
时,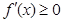 ,
,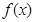 在
在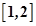 上为增函数,
上为增函数,
故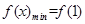
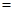
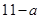 ,所以
,所以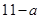
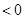 ,
,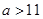 ,这与
,这与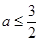 矛盾……………8分
矛盾……………8分
当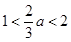 ,即
,即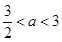 时,
时,
若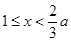 ,
,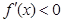 ;
;
若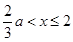 ,
,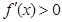 ,
,
所以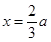 时,
时,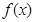 取最小值,
取最小值,
因此有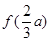
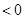 ,即
,即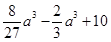
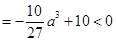 ,解得
,解得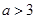 ,这与
,这与
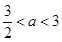 矛盾; ………………10分
矛盾; ………………10分
当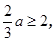 即
即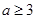 时,
时,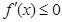 ,
,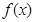 在
在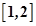 上为减函数,所以
上为减函数,所以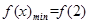
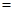
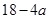 ,所以
,所以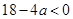 ,解得
,解得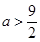 ,这符合
,这符合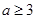 .
.
综上所述,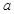 的取值范围为
的取值范围为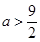 . ………………12分
. ………………12分
解2:有已知得: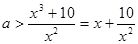 , ………………7分
, ………………7分
设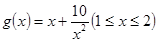 ,
,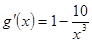 , ………………9分
, ………………9分
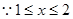 ,
,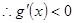 ,所以
,所以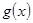 在
在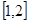 上是减函数. ………………10分
上是减函数. ………………10分
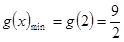 ,所以
,所以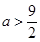 . ………………12分
. ………………12分
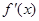 ,然后利用
,然后利用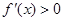 解出f(x)的单调递增区间.
解出f(x)的单调递增区间.(II)本小题的实质是求f(x)在[1,2]的最小值,根据f(x)的最小值小于零求a的取值范围.在求f(x)的最小值时,要利用导数解决.
(I)当
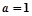 时,
时,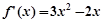
当
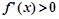 得
得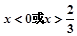
所以函数
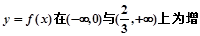
(II)解1:
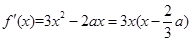
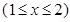
当
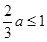 ,即
,即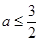 时,
时,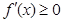 ,
,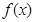 在
在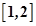 上为增函数,
上为增函数,故
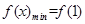
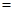
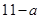 ,所以
,所以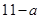
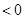 ,
,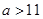 ,这与
,这与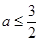 矛盾……………8分
矛盾……………8分当
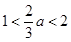 ,即
,即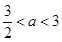 时,
时,若
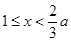 ,
,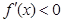 ;
;若
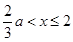 ,
,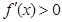 ,
,所以
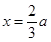 时,
时,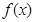 取最小值,
取最小值,因此有
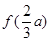
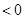 ,即
,即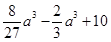
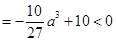 ,解得
,解得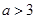 ,这与
,这与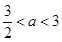 矛盾; ………………10分
矛盾; ………………10分当
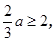 即
即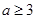 时,
时,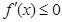 ,
,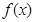 在
在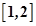 上为减函数,所以
上为减函数,所以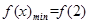
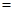
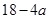 ,所以
,所以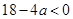 ,解得
,解得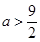 ,这符合
,这符合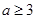 .
.综上所述,
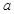 的取值范围为
的取值范围为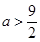 . ………………12分
. ………………12分解2:有已知得:
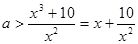 , ………………7分
, ………………7分设
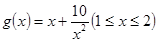 ,
,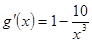 , ………………9分
, ………………9分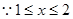 ,
,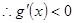 ,所以
,所以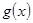 在
在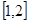 上是减函数. ………………10分
上是减函数. ………………10分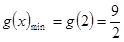 ,所以
,所以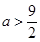 . ………………12分
. ………………12分
练习册系列答案
相关题目
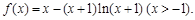
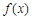 的单调区间;
的单调区间;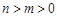 时,
时,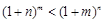 ;
;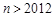 ,且
,且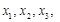 …,
…,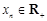 ,
,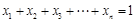 时,
时,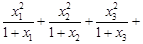 …
…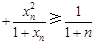
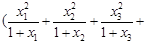 …
…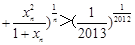 .
.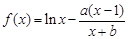 .
.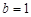 时,若函数
时,若函数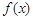 在
在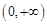 上为单调增函数,求
上为单调增函数,求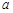 的取值范围;
的取值范围;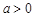 且
且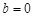 时,求证:函数f (x)存在唯一零点的充要条件是
时,求证:函数f (x)存在唯一零点的充要条件是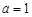 ;
;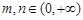 ,且
,且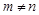 ,求证:
,求证: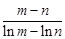 <
<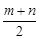 .
.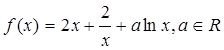 。
。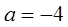 ,求函数
,求函数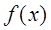 的单调区间;
的单调区间;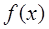 在
在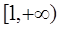 上单调递增,求实数
上单调递增,求实数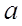 的取值范围;
的取值范围;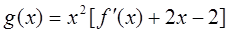 ,若
,若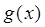 的最小值是
的最小值是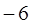 ,求函数
,求函数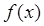 的解析式。
的解析式。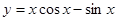 在下列哪个区间内是增函数( )
在下列哪个区间内是增函数( )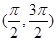
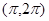
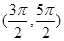
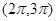
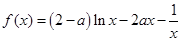 .
.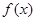 的单调性;
的单调性;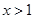 时,
时,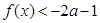 ,求实数
,求实数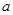 的取值范围;
的取值范围;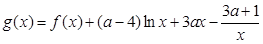 ,若
,若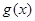 在区间
在区间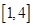 上不单调, 求实数
上不单调, 求实数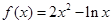 的递增区间是
的递增区间是