题目内容
下列关于函数f(x)=(2x-x2)ex的判断正确的是
①f(x)>0的解集是{x|0<x<2};
②f(-)是极小值,f()是极大值;
③f(x)没有最小值,也没有最大值.
①f(x)>0的解集是{x|0<x<2};
②f(-)是极小值,f()是极大值;
③f(x)没有最小值,也没有最大值.
| A.①③ | B.①② | C.② | D.①②③ |
B
′(x)=ex(2-x2),由f′(x)=0得x=±,
由f′(x)<0得x> 或x<- ,
由f′(x)>0得- <x< ,
∴f(x)的单调减区间为(-∞,- ),( ,+∞).单调增区间为(-, ).
∴f(x)的极大值为f( ),极小值为f(- ),故③不正确.
∵x<- 2 时,f(x)<0恒成立.
∴f(x)无最小值,但有最大值f( )
∴②正确④不正确..
故选B.
由f′(x)<0得x> 或x<- ,
由f′(x)>0得- <x< ,
∴f(x)的单调减区间为(-∞,- ),( ,+∞).单调增区间为(-, ).
∴f(x)的极大值为f( ),极小值为f(- ),故③不正确.
∵x<- 2 时,f(x)<0恒成立.
∴f(x)无最小值,但有最大值f( )
∴②正确④不正确..
故选B.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
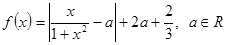
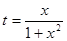 在
在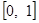 上的单调性;
上的单调性;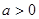 ,求函数
,求函数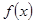 在
在 。
。 .
. 是函数
是函数 的极值点,求
的极值点,求 的值;
的值;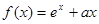 。
。 在
在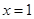 处的切线与直线
处的切线与直线 垂直,求
垂直,求 的值;
的值;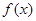 在区间(
在区间(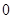 ,
,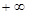 )内是增函数,求
)内是增函数,求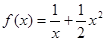 ,存在
,存在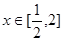 ,使得
,使得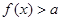 成立,则实数
成立,则实数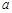 的取值范围是( )
的取值范围是( )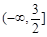
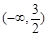

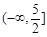
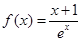 .
. 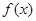 的单调区间;
的单调区间;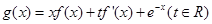 .是否存在实数
.是否存在实数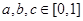 ,使得
,使得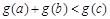 ?若存在,求实数
?若存在,求实数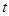 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.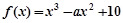 ,
,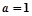 时,求函数
时,求函数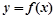 的单调递增区间;
的单调递增区间;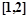 内至少存在一个实数
内至少存在一个实数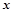 ,使得
,使得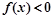 成立,求实数
成立,求实数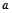 的取值范围.
的取值范围.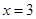 是函数
是函数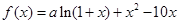 的一个极值点.
的一个极值点.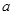 ;
;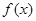 的单调区间.
的单调区间.