题目内容
设函数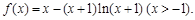
(Ⅰ)求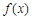 的单调区间;
的单调区间;
(Ⅱ)证明:当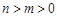 时,
时,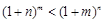 ;
;
(Ⅲ)证明:当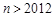 ,且
,且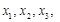 …,
…,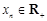 ,
,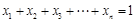 时,
时,
(1)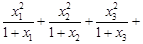 …
…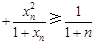
(2)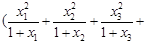 …
…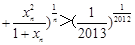 .
.
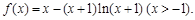
(Ⅰ)求
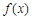 的单调区间;
的单调区间;(Ⅱ)证明:当
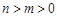 时,
时,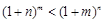 ;
;(Ⅲ)证明:当
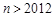 ,且
,且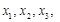 …,
…,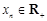 ,
,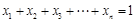 时,
时,(1)
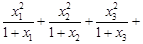 …
…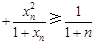
(2)
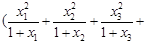 …
…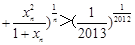 .
.(Ⅰ)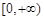 (Ⅱ)见解析(Ⅲ)见解析
(Ⅱ)见解析(Ⅲ)见解析
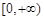 (Ⅱ)见解析(Ⅲ)见解析
(Ⅱ)见解析(Ⅲ)见解析本试题主要是考查了导数在研究函数中的运用。求解函数的单调区间和证明不等是的综合运用。
(1)先求解函数的定义域和函数的导数,然后结合导数的符号判定单调区间。
(2)运用第一问中的结论。得到不等式的放缩得到证明。
(3)结合第一问和第二问的基础上,进一步放缩法得到结论。
解:(Ⅰ)由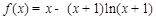 ,有
,有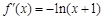 ,………………… 2分
,………………… 2分
当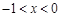 时,
时,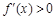 时,
时,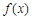 单调递增;
单调递增;
当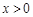 时,
时,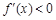 时,
时,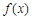 单调递减;
单调递减;
所以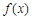 的单调递增区间为
的单调递增区间为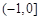 ,单调递减区间为
,单调递减区间为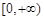 . …… 4分
. …… 4分
(Ⅱ)设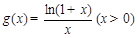 ,
,
则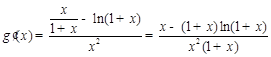 .………………6分
.………………6分
由(Ⅰ)知,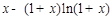 在
在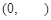 单调递减,
单调递减,
∴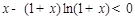 ,即
,即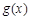 是减函数,
是减函数,
而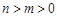 ,所以
,所以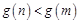 ,得
,得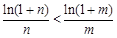 ,
,
得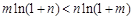 ,故
,故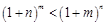 .………………… 8分
.………………… 8分
(Ⅲ)(1)由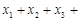 …
…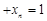 ,及柯西不等式可知,
,及柯西不等式可知,
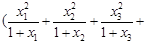 …
…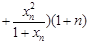
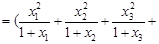 …
…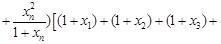 …
…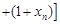
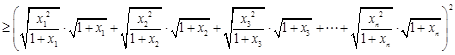
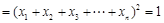 ,
,
所以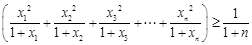 ,……………………11分
,……………………11分
(2)由(1)得: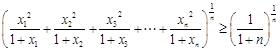 .
.
又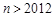 ,由(Ⅱ)可知
,由(Ⅱ)可知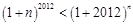 ,
,
即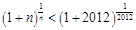 ,即
,即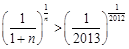 .
.
则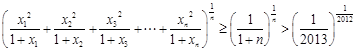 .
.
故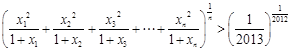 ………………14分
………………14分
(1)先求解函数的定义域和函数的导数,然后结合导数的符号判定单调区间。
(2)运用第一问中的结论。得到不等式的放缩得到证明。
(3)结合第一问和第二问的基础上,进一步放缩法得到结论。
解:(Ⅰ)由
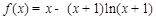 ,有
,有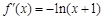 ,………………… 2分
,………………… 2分当
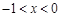 时,
时,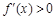 时,
时,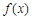 单调递增;
单调递增;当
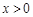 时,
时,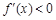 时,
时,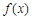 单调递减;
单调递减;所以
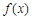 的单调递增区间为
的单调递增区间为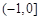 ,单调递减区间为
,单调递减区间为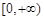 . …… 4分
. …… 4分(Ⅱ)设
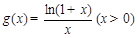 ,
,则
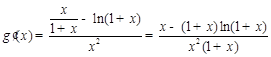 .………………6分
.………………6分由(Ⅰ)知,
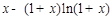 在
在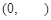 单调递减,
单调递减,∴
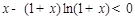 ,即
,即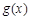 是减函数,
是减函数,而
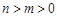 ,所以
,所以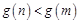 ,得
,得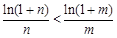 ,
,得
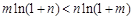 ,故
,故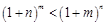 .………………… 8分
.………………… 8分(Ⅲ)(1)由
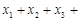 …
…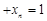 ,及柯西不等式可知,
,及柯西不等式可知,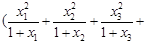 …
…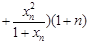
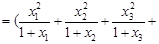 …
…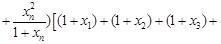 …
…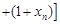
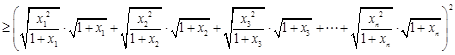
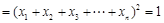 ,
, 所以
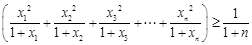 ,……………………11分
,……………………11分(2)由(1)得:
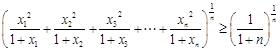 .
. 又
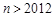 ,由(Ⅱ)可知
,由(Ⅱ)可知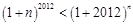 ,
,即
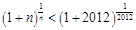 ,即
,即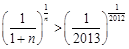 .
.则
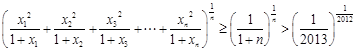 .
.故
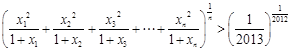 ………………14分
………………14分
练习册系列答案
相关题目
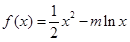 (m
(m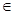 R)
R) 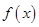 在
在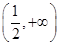 上单调递增,求实数
上单调递增,求实数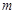 的取值范围;
的取值范围;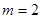 时,求函数
时,求函数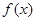 在
在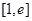 上的最大,最小值;
上的最大,最小值;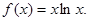
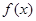 的单调区间和最小值;
的单调区间和最小值;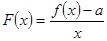 在
在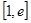 上是最小值为
上是最小值为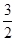 ,求
,求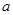 的值;
的值;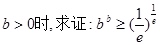 (其中
(其中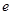 ="2.718" 28…是自然对数的底数).
="2.718" 28…是自然对数的底数).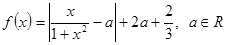
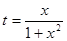 在
在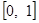 上的单调性;
上的单调性;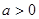 ,求函数
,求函数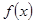 在
在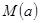 。
。 ,在
,在 上单调递增,在
上单调递增,在 上单调递减
上单调递减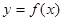 在定义域(-
在定义域(-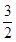 ,3)内可导,其图象如图所示,记
,3)内可导,其图象如图所示,记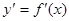 ,则不等式
,则不等式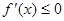 的解集为( )
的解集为( )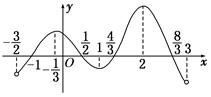
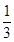 ,1]∪[2,3)
,1]∪[2,3) ]∪[
]∪[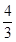 ,
,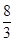 ]
] .
. 是函数
是函数 的极值点,求
的极值点,求 的值;
的值;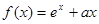 。
。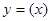 在
在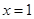 处的切线与直线
处的切线与直线 垂直,求
垂直,求 的值;
的值;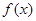 在区间(
在区间(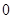 ,
,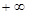 )内是增函数,求
)内是增函数,求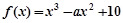 ,
,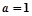 时,求函数
时,求函数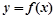 的单调递增区间;
的单调递增区间;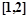 内至少存在一个实数
内至少存在一个实数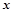 ,使得
,使得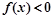 成立,求实数
成立,求实数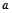 的取值范围.
的取值范围.