题目内容
(本小题10分)已知函数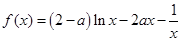 .
.
(1)试讨论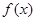 的单调性;
的单调性;
(2)如果当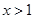 时,
时,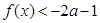 ,求实数
,求实数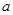 的取值范围;
的取值范围;
(3)记函数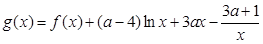 ,若
,若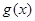 在区间
在区间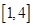 上不单调, 求实数
上不单调, 求实数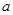 的取值范围.
的取值范围.
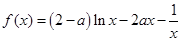 .
.(1)试讨论
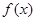 的单调性;
的单调性;(2)如果当
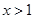 时,
时,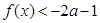 ,求实数
,求实数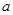 的取值范围;
的取值范围;(3)记函数
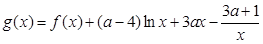 ,若
,若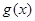 在区间
在区间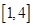 上不单调, 求实数
上不单调, 求实数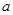 的取值范围.
的取值范围.解:(1)①若
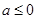 ,则
,则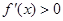 ,所以
,所以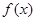 在
在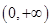 上单调递增
上单调递增②若
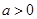 ,则由
,则由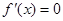 ,得
,得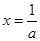 ,且当
,且当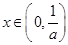 时,
时,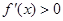 ,当
,当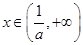 时,
时,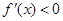 ,所以
,所以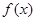 在
在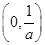 上单调递增,在
上单调递增,在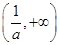 上单调递减;
上单调递减;(2)
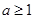 ;(3)
;(3)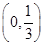 .
. 本试题主要是考查了导数在研究函数中的运用。解决不等式的恒成立问题,和函数的单调性的逆向运用的综合试题。
(1)首先求解导数,根据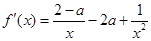
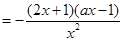 的分子为含有参数的二次函数,那么结合二次不等式进行分情况讨论得到单调区间。
的分子为含有参数的二次函数,那么结合二次不等式进行分情况讨论得到单调区间。
(2)利用当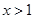 时,
时,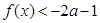 ,结合上一问的单调性,确定最值,解得a的范围。
,结合上一问的单调性,确定最值,解得a的范围。
(3)利用等价转化思想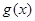 在区间
在区间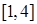 上不单调
上不单调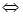

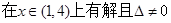 ,然后分离变量求解参数的取值范围。
,然后分离变量求解参数的取值范围。
解:(1)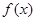 的定义域为
的定义域为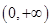 ,
,
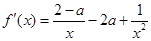
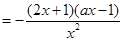 ……2分
……2分
①若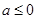 ,则
,则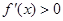 ,所以
,所以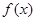 在
在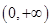 上单调递增
上单调递增
②若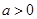 ,则由
,则由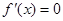 ,得
,得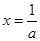 ,且当
,且当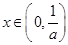 时,
时,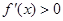 ,当
,当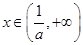 时,
时,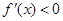 ,所以
,所以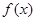 在
在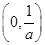 上单调递增,在
上单调递增,在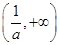 上单调递减; ……4分
上单调递减; ……4分
(2)由(1)知:
①若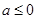 时,
时,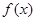 在
在 上单调递增,所以
上单调递增,所以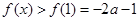 ,不合;
,不合;
②若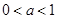 时,
时, 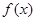 在
在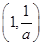 上单调递增,在
上单调递增,在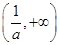 上单调递减;所以
上单调递减;所以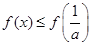 ,又
,又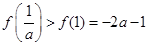 ,不合;
,不合;
③若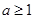 时,
时, 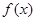 在
在 上单调递减;所以
上单调递减;所以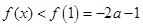 ,
,
综上所述, …………7分
…………7分
(3)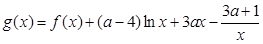
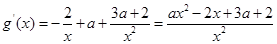
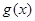 在区间
在区间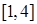 上不单调
上不单调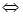

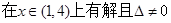
变量分离得,
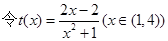 ,求得
,求得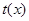 的值域为
的值域为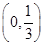
 ……10分
……10分
(1)首先求解导数,根据
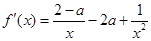
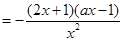 的分子为含有参数的二次函数,那么结合二次不等式进行分情况讨论得到单调区间。
的分子为含有参数的二次函数,那么结合二次不等式进行分情况讨论得到单调区间。(2)利用当
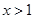 时,
时,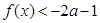 ,结合上一问的单调性,确定最值,解得a的范围。
,结合上一问的单调性,确定最值,解得a的范围。(3)利用等价转化思想
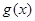 在区间
在区间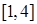 上不单调
上不单调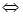

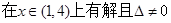 ,然后分离变量求解参数的取值范围。
,然后分离变量求解参数的取值范围。解:(1)
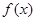 的定义域为
的定义域为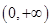 ,
,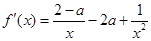
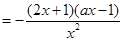 ……2分
……2分①若
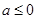 ,则
,则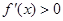 ,所以
,所以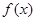 在
在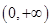 上单调递增
上单调递增②若
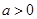 ,则由
,则由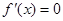 ,得
,得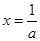 ,且当
,且当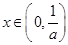 时,
时,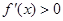 ,当
,当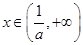 时,
时,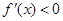 ,所以
,所以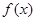 在
在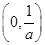 上单调递增,在
上单调递增,在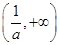 上单调递减; ……4分
上单调递减; ……4分(2)由(1)知:
①若
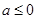 时,
时,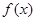 在
在 上单调递增,所以
上单调递增,所以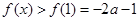 ,不合;
,不合;②若
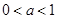 时,
时, 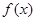 在
在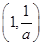 上单调递增,在
上单调递增,在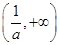 上单调递减;所以
上单调递减;所以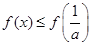 ,又
,又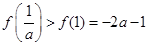 ,不合;
,不合;③若
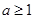 时,
时, 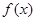 在
在 上单调递减;所以
上单调递减;所以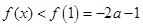 ,
,综上所述,
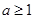 …………7分
…………7分(3)
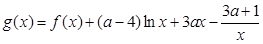
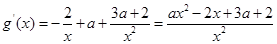
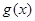 在区间
在区间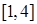 上不单调
上不单调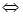

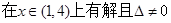
变量分离得,

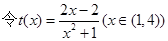 ,求得
,求得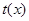 的值域为
的值域为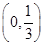
 ……10分
……10分
练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
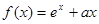 。
。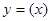 在
在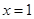 处的切线与直线
处的切线与直线 垂直,求
垂直,求 的值;
的值;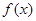 在区间(
在区间(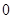 ,
,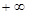 )内是增函数,求
)内是增函数,求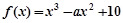 ,
,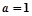 时,求函数
时,求函数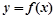 的单调递增区间;
的单调递增区间;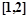 内至少存在一个实数
内至少存在一个实数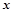 ,使得
,使得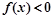 成立,求实数
成立,求实数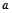 的取值范围.
的取值范围.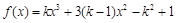 在区间(0,3)是增函数,则k的取值范围是( )
在区间(0,3)是增函数,则k的取值范围是( )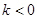
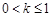
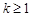

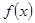 的定义域为
的定义域为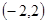 ,导函数为
,导函数为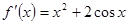 且
且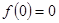 ,则满足
,则满足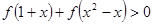 的实数
的实数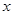 的取值范围为( )
的取值范围为( )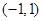
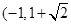 )
)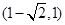
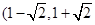 )
)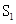 为直线
为直线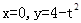 (
(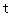 为常数)及
为常数)及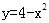 所围成的图形的面积,
所围成的图形的面积,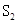 为直线
为直线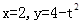 (
(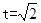 时,求
时,求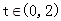 ,求
,求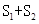 的最小值。
的最小值。
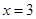 是函数
是函数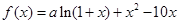 的一个极值点.
的一个极值点.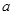 ;
;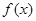 的单调区间.
的单调区间.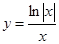 的图象大致是( )
的图象大致是( )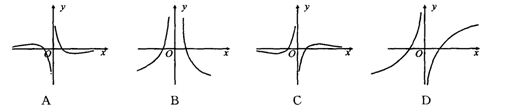
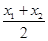 时,又称AB存在“中值伴随切线”.试问:在函数f(x)的图像上是否存在不同两点A,B,使得AB存在“中值伴随切线”?若存在,求出A,B的坐标;若不存在,说明理由
时,又称AB存在“中值伴随切线”.试问:在函数f(x)的图像上是否存在不同两点A,B,使得AB存在“中值伴随切线”?若存在,求出A,B的坐标;若不存在,说明理由