题目内容
【题目】数列![]() 的前
的前![]() 项1,3,7,
项1,3,7,![]() ,
,![]() (
(![]() )组成集合
)组成集合![]() ,从集合
,从集合![]() 中任取
中任取![]() (
(![]() )个数,其所有可能的
)个数,其所有可能的![]() 个数的乘积的和为
个数的乘积的和为![]() (若只取一个数,规定乘积为此数本身),记
(若只取一个数,规定乘积为此数本身),记![]() .例如:当
.例如:当![]() 时,
时,![]() ,
,![]() ,
,![]() ;
;![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,求
时,求![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)证明:![]() 时集合
时集合![]() 的
的![]() 与
与![]() 时集合
时集合![]() 的
的![]() (为以示区别,用
(为以示区别,用![]() 表示)有关系式
表示)有关系式![]() (
(![]() ,
,![]() );
);
(3)试求![]() (用
(用![]() 表示).
表示).
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() (2)见解析(3)
(2)见解析(3)![]()
【解析】
(1)当![]() 时,得出
时,得出![]() ,根据定义得出
,根据定义得出![]() 、
、![]() 、
、![]() 的值,可计算出
的值,可计算出![]() 的值;
的值;
(2)当![]() 时,集合
时,集合![]() 有
有![]() 个元素,比
个元素,比![]() 时的集合
时的集合![]() 多了一个元素;
多了一个元素;
![]() ,对应的
,对应的![]() 包含两个部分:(i)若
包含两个部分:(i)若![]() 不含
不含![]() ,则
,则![]() 中的任何一项恰好为
中的任何一项恰好为![]() 时集合
时集合![]() 的对应的
的对应的![]() 中的一项;(ii)若
中的一项;(ii)若![]() 中含
中含![]() 的任何一项,除了
的任何一项,除了![]() ,其余的
,其余的![]() 个数均来自集合
个数均来自集合![]() ,这
,这![]() 个数的乘积恰好为集合
个数的乘积恰好为集合![]() 所对应的
所对应的![]() 中的一项,即可证明;
中的一项,即可证明;
(3)由![]() ,
,![]() ,
,![]() ,猜想
,猜想![]() ,下面利用数学归纳法进行即可.
,下面利用数学归纳法进行即可.
(1)当![]() 时,
时,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]()
(2)证明:当![]() 时,集合
时,集合![]() 有
有![]() 个元素,比
个元素,比![]() 时的集合
时的集合![]() 多了一个元素:
多了一个元素:![]() .∴对应的
.∴对应的![]() 包含两个部分:
包含两个部分:
若![]() 中不含
中不含![]() ,则
,则![]() 中的任何一项恰好为
中的任何一项恰好为![]() 时集合
时集合![]() 的对应的
的对应的![]() 中的一项.
中的一项.
若![]() 中含
中含![]() 的任何一项,除了
的任何一项,除了![]() ,其余的
,其余的![]() 个数均来自集合
个数均来自集合![]() ,这
,这![]() 个数的乘积恰好为集合
个数的乘积恰好为集合![]() 所对应的
所对应的![]() 中的一项.
中的一项.
∴有关系式![]()
(3)解:由![]() ,
,![]() ,
,![]() ,
,
猜想![]() .下面证明:(i)易知
.下面证明:(i)易知![]() 时成立.
时成立.
(ii)假设![]() 时,
时,![]() ,
,
则![]() 时,
时,![]()
![]()
(其中![]() ,
,![]() ,2,…,k,为
,2,…,k,为![]() 时可能的k个数的乘积的和为
时可能的k个数的乘积的和为![]() ,
,
![]()
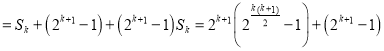
![]() ,即
,即![]() 时,
时,![]() 也成立,
也成立,
综合(i)(ii)知对![]() ,
,![]() 成立.
成立.
∴![]() .
.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
【题目】某工厂因排污比较严重,决定着手整治,一个月时污染度为![]() ,整治后前四个月的污染度如下表:
,整治后前四个月的污染度如下表:
月数 |
|
|
|
| … |
污染度 |
|
|
|
| … |
污染度为![]() 后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:
后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:![]() ,
,![]() ,
,![]() ,其中
,其中![]() 表示月数,
表示月数,![]() 、
、![]() 、
、![]() 分别表示污染度.
分别表示污染度.
(1)问选用哪个函数模拟比较合理,并说明理由;
(2)若以比较合理的模拟函数预测,整治后有多少个月的污染度不超过![]() .
.