题目内容
【题目】某厂生产某种产品的年固定成本为250万元,每生产![]() 千件,需另投入成本
千件,需另投入成本![]() ,当年产量不足80千件时,
,当年产量不足80千件时,![]() (万元);当年产量不小于80千件时,
(万元);当年产量不小于80千件时,![]() (万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
【答案】(1)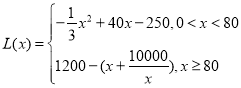 ;(2)100千件.
;(2)100千件.
【解析】
(1)分两种情况进行研究,当![]() 时,当
时,当![]() 时,分别根据年利润等于销售收入与成本的差,列出函数关系式,最后写成分段函数的形式,从而得到答案;(2)根据年利润的解析式,分段研究函数的最值,当
时,分别根据年利润等于销售收入与成本的差,列出函数关系式,最后写成分段函数的形式,从而得到答案;(2)根据年利润的解析式,分段研究函数的最值,当![]() 时,利用二次函数求最值,当
时,利用二次函数求最值,当![]() 时,利用基本不等式求最值,最后比较两个最值,即可得到答案.
时,利用基本不等式求最值,最后比较两个最值,即可得到答案.
(1)∵每件商品售价为0.05万元,
∴![]() 千件商品销售额为
千件商品销售额为![]() 万元,
万元,
①当![]() 时,根据年利润=销售收入-成本,
时,根据年利润=销售收入-成本,
∴![]() ;
;
②当![]() 时,根据年利润=销售收入-成本,
时,根据年利润=销售收入-成本,
∴![]()
综合①②可得,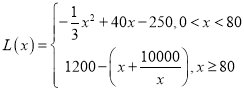 ;
;
(2)①当![]() 时,
时,![]() ,
,
∴当![]() 时,
时,![]() 取得最大值
取得最大值![]() 万元;
万元;
②当![]() 时,
时,![]() ,
,
当且仅当![]() ,即
,即![]() 时,
时,![]() 取得最大值
取得最大值![]() 万元.
万元.
综合①②,由于![]() ,
,
∴年产量为100千件时,该厂在这一商品的生产中所获利润最大.

【题目】随机观测生产某种零件的某工作厂25名工人的日加工零件个数(单位:件),获得数据如下:30,42,41,36,44,40,37,37,25,45,29,43,31,36,49,34,33,43,38,42,32,34,46,39,36.根据上述数据得到样本的频率分布表如下:
分组 | 频数 | 频率 |
[25,30] | 3 | 0.12 |
(30,35] | 5 | 0.20 |
(35,40] | 8 | 0.32 |
(40,45] | n1 | f1 |
(45,50] | n2 | f2 |
(1)确定样本频率分布表中n1 , n2 , f1和f2的值;
(2)根据上述频率分布表,画出样本频率分布直方图;
(3)根据样本频率分布直方图,求在该厂任取4人,至少有1人的日加工零件数落在区间(30,35]的概率.
