[题目]已知等差数列满足且.等比数列的首项为2.公比为.(1)若.问等于数列中的第几项?(2)若.数列和的前项和分别记为和.的最大值为.试比较与的大小. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知等差数列满足且，等比数列的首项为2，公比为.

（1）若，问等于数列中的第几项？

（2）若，数列和的前项和分别记为和，的最大值为，试比较与的大小.

【答案】(1) (2)

【解析】

(1)根据等差数列的通项公式,即可求得数列的通项公式.根据等比数列的首项与公比,求得等比数列的通项公式,进而可求得.即可求出等于数列中项.

(2)根据等差数列的求和公式即可求得等差数列前项和的最大值为.由等比数列的前项和公式求得的值,即可比较与的大小.

(1) 因为等差数列满足

即,所以等差数列的公差

又

得,代入可得

所以

当等比数列的首项为2,公比为.

当时

所以

所以当时

解得

即时等于数列中的第16项

(2) 等比数列的首项为2,若

由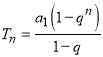可得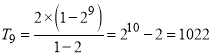

又等差数列中代入可得

所以当时, 的最大值为

所以

练习册系列答案

相关题目

【题目】定义函数，数列满足，.

（1）若，求及；

（2）若且数列为周期函数，且最小正周期，求的值；

（3）是否存在，使得成等比数列？若存在，求出所有这样的，若不存在，说明理由.

【题目】已知圆，是圆M内一定点，动点P为圆M上任意一点，线段PN的垂直平分线l和半径MP相交于点C.

（1）求点C的轨迹方程；

（2）设直线与C交于不同两点A，B，点O为坐标原点，当的面积S取最大值时，求的值.

【题目】设数列A：， ,… ().如果对小于()的每个正整数都有＜，则称是数列A的一个“G时刻”.记“是数列A的所有“G时刻”组成的集合.

（1）对数列A：-2，2，-1，1，3，写出的所有元素；

（2）证明：若数列A中存在使得>，则；

（3）证明：若数列A满足- ≤1（n=2,3, …,N）,则的元素个数不小于 -.

【题目】心理学研究表明，人极易受情绪的影响，某选手参加7局4胜制的兵乒球比赛.

（1）在不受情绪的影响下，该选手每局获胜的概率为；但实际上，如果前一句获胜的话，此选手该局获胜的概率可提升到；而如果前一局失利的话，此选手该局获胜的概率则降为，求该选手在前3局获胜局数的分布列及数学期望；

（2）假设选手的三局比赛结果互不影响，且三局比赛获胜的概率为，记为锐角的内角，求证：

【题目】如果函数的定义域为，且存在实常数a，使得对于定义域内任意x，都成立，则称此函数具有“性质”

（1）判断函数是否具有“性质”，若具有“性质”，求出所有a的值的集合；若不具有“性质”，请说明理由；

（2）已知函数具有“性质”，且当时，，求函数在区间上的值域；

（3）已知函数具有“性质”，又具有“性质”，且当时，，若函数的图像与直线有2017个公共点，求实数p的值.

【题目】如图，在三棱锥中，平面平面，为等边三角形，，是的中点.

（1）证明：；

（2）若，求二面角平面角的余弦值.

【题目】如图，直四棱柱底面直角梯形，∥，，是棱上一点，，，，，.

（1）求异面直线与所成的角；

（2）求证：平面.

【题目】某公司为了了解年研发资金投人量（单位：亿元）对年销售额（单位：亿元）的影响.对公司近年的年研发资金投入量和年销售额的数据，进行了对比分析，建立了两个函数模型：①，②，其中、、、均为常数，为自然对数的底数.并得到一些统计量的值.令，，经计算得如下数据：

（1）请从相关系数的角度，分析哪一个模型拟合程度更好？

（2）（ⅰ）根据（1）的选择及表中数据，建立关于的回归方程；

（ⅱ）若下一年销售额需达到亿元，预测下一年的研发资金投入量是多少亿元？

附：①相关系数，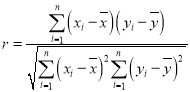

回归直线中公式分别为：，；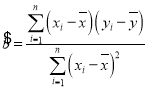

②参考数据：，，.

试题分类