题目内容
【题目】定义函数![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 及
及![]() ;
;
(2)若![]() 且数列
且数列![]() 为周期函数,且最小正周期
为周期函数,且最小正周期![]() ,求
,求![]() 的值;
的值;
(3)是否存在![]() ,使得
,使得![]() 成等比数列?若存在,求出所有这样的
成等比数列?若存在,求出所有这样的![]() ,若不存在,说明理由.
,若不存在,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() ,理由见解析
,理由见解析
【解析】
(1)对于分别取n=1,2,an+1=f(an),n∈N*.去掉绝对值符号即可得出;
(2)由已知可得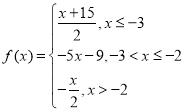 ,分三种情况讨论即可求值;
,分三种情况讨论即可求值;
(3)假设存在a1,使得a1,a2,…,an,…成等比数列,分类讨论当![]() 及当
及当![]() 和
和![]() 时,分别利用递推关系及等比数列的定义,得出a1的取值范围.
时,分别利用递推关系及等比数列的定义,得出a1的取值范围.
(1)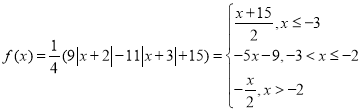 ,
,
∴a2=f(a1)=f(﹣30)=![]() ,
,
a3=f(a2)=f(![]() )=
)=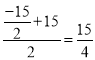 .
.
(2)由已知可得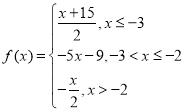 ,
,
由题意数列![]() 为周期函数,且最小正周期
为周期函数,且最小正周期![]() ,
,
则当![]() 时,a2=f(a1)=
时,a2=f(a1)=![]() ;a3=f(a2)=f(
;a3=f(a2)=f(![]() )=
)=![]() ,
,
得到![]() (舍);
(舍);
当![]() 时,a2=f(a1)=
时,a2=f(a1)=![]() ;a3=f(a2)=f(
;a3=f(a2)=f(![]() )=
)=![]() ,
,
得到![]() (舍);
(舍);
当![]() 时,a2=f(a1)=
时,a2=f(a1)=![]() ;
;
a3=f(a2)=f( f(a1))=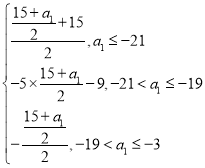 ,
,
令a3=a1,则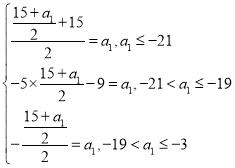
则a1=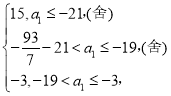
综上得到![]() ;
;
(3)假设存在a1,使得a1,a2,…,an,…成等比数列.
①当![]() 时,a2=f(a1)=
时,a2=f(a1)=![]() ;a3=f(a2)=
;a3=f(a2)=![]() ,
,
则公比为![]() ,∴a2=
,∴a2=![]() ,则
,则![]() ,则
,则![]() 满足题意;
满足题意;
②当a1![]() 时,则a2=f(a1)=
时,则a2=f(a1)=![]() ,则必存在k使得
,则必存在k使得![]() ,
,
若![]() ,由①知
,由①知![]() ;
;
若![]() ,
,![]() ∴
∴![]() ∴
∴![]() ,则
,则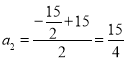 ,
,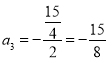
![]() ,满足
,满足![]() ,满足公比为
,满足公比为![]()
综上可知:a1的取值范围为 [﹣2,+∞).

【题目】为发挥体育核心素养的独特育人价值,越来越多的中学将某些体育项目纳入到学生的必修课程.惠州市某中学计划在高一年级开设游泳课程,为了解学生对游泳的兴趣,某数学研究学习小组随机从该校高一年级学生中抽取了100人进行调查.
(1)已知在被抽取的学生中高一![]() 班学生有6名,其中3名对游泳感兴趣,现在从这6名学生中随机抽取3人,求至少有2人对游泳感兴趣的概率;
班学生有6名,其中3名对游泳感兴趣,现在从这6名学生中随机抽取3人,求至少有2人对游泳感兴趣的概率;
(2)该研究性学习小组在调查中发现,对游泳感兴趣的学生中有部分曾在市级或市级以上游泳比赛中获奖,具体获奖人数如下表所示.若从高一![]() 班和高一
班和高一![]() 班获奖学生中随机各抽取2人进行跟踪调查,记选中的4人中市级以上游泳比赛获奖的人数为
班获奖学生中随机各抽取2人进行跟踪调查,记选中的4人中市级以上游泳比赛获奖的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
班级 | 一 | 一 | 一 | 一 | 一 | 一 | 一 | 一 | 一 | 一 |
|
市级 比赛获奖人数 | 2 | 2 | 3 | 3 | 4 | 4 | 3 | 3 | 4 | 2 |
|
市级以上 比赛获奖人数 | 2 | 2 | 1 | 0 | 2 | 3 | 3 | 2 | 1 | 2 |
|