题目内容
如图,在四棱锥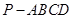 中,顶点
中,顶点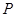 在底面
在底面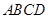 内的射影恰好落在
内的射影恰好落在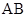 的中点
的中点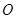 上,又
上,又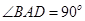 ,
,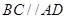 且
且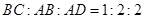
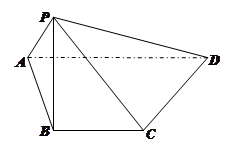
(1)求证: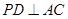 ;
;
(2)若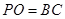 ,求直线
,求直线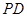 与
与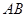 所成角的余弦值;
所成角的余弦值;
(3)若平面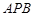 与平面
与平面 所成的角为
所成的角为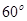 ,求
,求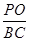 的值。
的值。
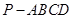 中,顶点
中,顶点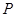 在底面
在底面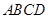 内的射影恰好落在
内的射影恰好落在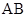 的中点
的中点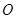 上,又
上,又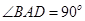 ,
,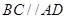 且
且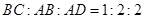
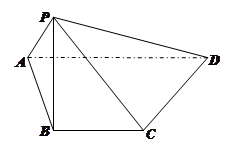
(1)求证:
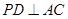 ;
;(2)若
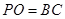 ,求直线
,求直线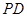 与
与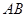 所成角的余弦值;
所成角的余弦值;(3)若平面
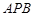 与平面
与平面 所成的角为
所成的角为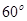 ,求
,求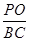 的值。
的值。(1)利用两直线的方向向量垂直证明线线垂直;(2) ;(3)
;(3)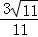 .
.
 ;(3)
;(3)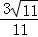 .
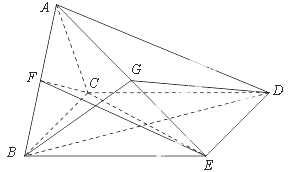
.试题分析:因为AB中点O为点P在平面ABCD内的射影,所以PO⊥底面ABCD.以O为坐标原点,AB所在直线为x轴,OP所在直线为z轴,建立空间直角坐标系o﹣xyz(如图).

(1)设BC=a,OP=h则依题意得:B(a,0,0),A(﹣a,0,0),P(0,0,h),C(a,a,0),D(﹣a,2a,0).
∴
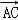 =(2a,a,0),
=(2a,a,0),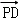 =(﹣a,2a,﹣h),
=(﹣a,2a,﹣h),于是
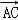 •
•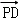 =﹣2a2+2a2=0,∴PD⊥AC; 4分
=﹣2a2+2a2=0,∴PD⊥AC; 4分(2)由PO=BC,得h=a,于是P(0,0,a),5分
∵
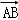 =(2a, 0,0),
=(2a, 0,0),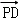 =(﹣a,2a,﹣a),
=(﹣a,2a,﹣a),∴
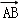 •
• =﹣2a2,cos<
=﹣2a2,cos<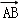 ,
, >=
>= =
= ,
,∴直线PD与AB所成的角的余弦值为
 ; -8分
; -8分(3)设平面PAB的法向量为m,可得m=(0,1,0),
设平面PCD的法向量为n=(x,y,z),
由
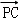 =(a,a,﹣h),
=(a,a,﹣h), =(﹣a,2a,﹣h),
=(﹣a,2a,﹣h),∴
 ,解得n=(1,2,
,解得n=(1,2, ),∴m•n=2,
),∴m•n=2,cos<m,n>=
 ,∵二面角为60°,∴
,∵二面角为60°,∴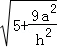 =4,
=4,解得=
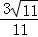 ,即
,即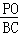 =
=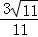 . 12分
. 12分点评:运用向量在解决立体几何问题主要集中在法向量的应用上,它可以证明空间线面的位置关系、求解空间角、距离.同时运用空间向量解答立体几何问题,淡化了传统立体几何中的“形”的推理方法,强化了代数运算,从而降低了思维难度

练习册系列答案
相关题目
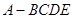 中,
中,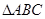 是正三角形,四边形
是正三角形,四边形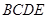 是矩形,且平面
是矩形,且平面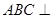 平面
平面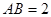 ,
,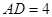 .
.
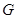 是
是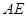 的中点,求证:
的中点,求证: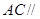 平面
平面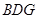 ;
;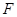 在线段
在线段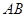 上什么位置时,二面角
上什么位置时,二面角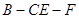 的余弦值为
的余弦值为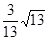 .
. 中,
中,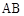
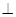 平面
平面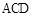 ,
,
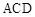 ,
,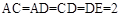 ,
, 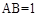 ,
,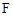 为
为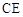 的中点
的中点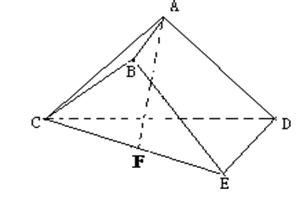
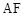
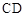 ;
;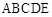 的体积.
的体积.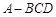 中,
中, ,
,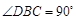 ,
,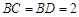 ,
,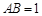 ,则BC和平面ACD所成角的正弦值为 .
,则BC和平面ACD所成角的正弦值为 .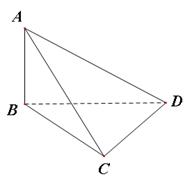
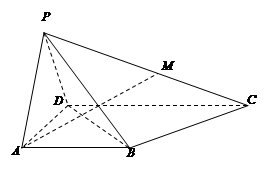
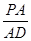 多大时,AM⊥平面PDB可能成立?
多大时,AM⊥平面PDB可能成立?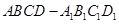 中,底面
中,底面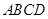 为平行四边形,且
为平行四边形,且 ,
,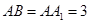 ,
,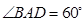 ,
,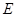 为
为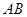 的中点.
的中点.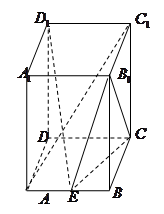
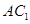 ∥平面
∥平面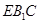 ;
;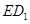 与平面
与平面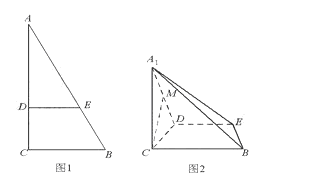
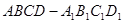 中,
中,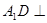 平面
平面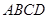 ,底面
,底面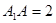 ,
,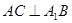 ;
;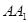 上存在一点
上存在一点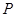 ,使得
,使得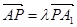 ,
,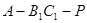 的大小为
的大小为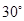 时,求实数
时,求实数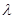 的值.
的值.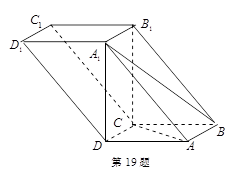
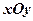 中,方程
中,方程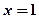 表示过点
表示过点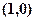 且平行于
且平行于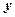 轴的直线。类比以上结论有:在空间直角坐标系
轴的直线。类比以上结论有:在空间直角坐标系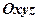 中,方程
中,方程