题目内容
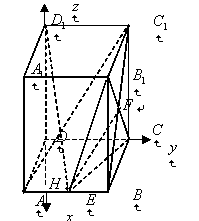
如图,在直四棱柱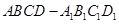 中,底面
中,底面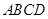 为平行四边形,且
为平行四边形,且 ,
,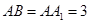 ,
,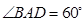 ,
,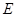 为
为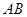 的中点.
的中点.
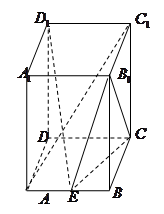
(1) 证明: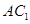 ∥平面
∥平面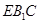 ;
;
(2)求直线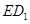 与平面
与平面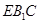 所成角的正弦值.
所成角的正弦值.
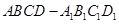 中,底面
中,底面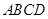 为平行四边形,且
为平行四边形,且 ,
,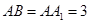 ,
,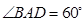 ,
,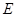 为
为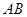 的中点.
的中点.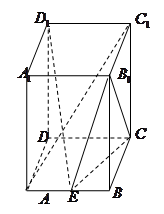
(1) 证明:
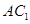 ∥平面
∥平面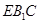 ;
;(2)求直线
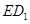 与平面
与平面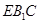 所成角的正弦值.
所成角的正弦值.(1)利用线线平行证明线面平行;(2)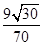
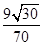
试题分析:(1) 证明:连接
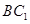 ,
,
因为
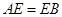 ,
,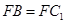 ,所以
,所以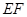 ∥
∥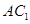 ,
,因为
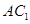
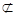 面
面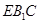 ,
,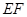
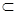 面
面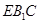 ,所以
,所以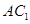 ∥面
∥面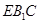 .
.(2)作
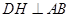 ,分别令
,分别令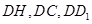 为
为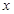 轴,
轴,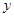 轴,
轴,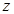 轴,建立坐标系如图
轴,建立坐标系如图因为
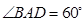 ,
, ,所以
,所以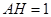 ,
, 、
、
所以
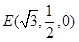 ,
,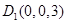 ,
,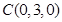 ,
,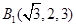 ,
,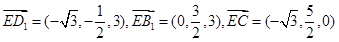
设面
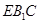 的法向量为
的法向量为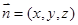 ,所以
,所以 ,
,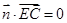
化简得
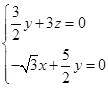 ,令
,令 ,则
,则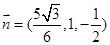 .
.设
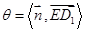 ,则
,则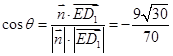
设直线
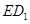 与面
与面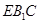 所成角为
所成角为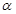 ,则
,则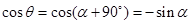
所以
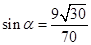 ,则直线
,则直线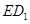 与面
与面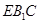 所成角的正弦值为
所成角的正弦值为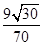 .
.点评:(1)线面关系的证明主要是应用线面平行与垂直的判定定理或性质,具体问题中要是能够根据题意适当做辅助线;(2)空间中角的计算,总是通过一定的手段将其转化为一个平面内的角,并把它置于一个平面图形,而且是一个三角形的内角来解决,而这种转化就是利用直线与平面的平行与垂直来实现的

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
 ABCD的底面是正方形,每条侧棱的长都是底面边长的
ABCD的底面是正方形,每条侧棱的长都是底面边长的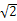 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点.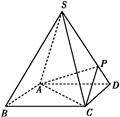
 为何值时,二面角A -A1D - C的平面角为600.
为何值时,二面角A -A1D - C的平面角为600.
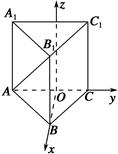
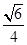
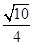
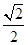
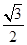
 的棱长为
的棱长为 ,
, 、
、 分别是
分别是 、
、 的中点.
的中点.
 的体积;
的体积; 与平面
与平面 所成角的余弦值.
所成角的余弦值. 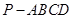 中,顶点
中,顶点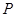 在底面
在底面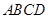 内的射影恰好落在
内的射影恰好落在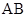 的中点
的中点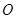 上,又
上,又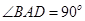 ,
,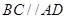 且
且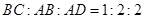
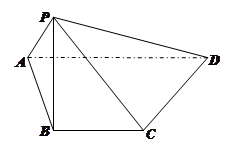
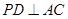 ;
;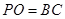 ,求直线
,求直线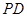 与
与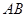 所成角的余弦值;
所成角的余弦值;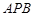 与平面
与平面 所成的角为
所成的角为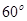 ,求
,求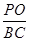 的值。
的值。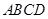 的边长为
的边长为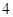 ,
,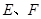 分别是
分别是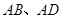 的中点,
的中点,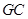 ⊥平面
⊥平面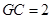 ,则点
,则点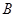 到平面
到平面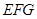 的距离为
的距离为 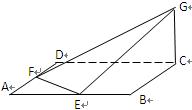
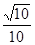
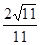
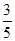
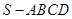 中,底面
中,底面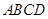 为平行四边形,
为平行四边形,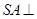 底面
底面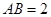 ,
,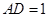 ,
,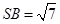 ,
,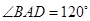 ,E在棱
,E在棱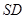 上, (Ⅰ) 当
上, (Ⅰ) 当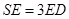 时,求证:
时,求证: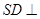 平面
平面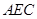 ; (Ⅱ) 当二面角
; (Ⅱ) 当二面角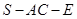 的大小为
的大小为 时,求直线
时,求直线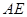 与平面
与平面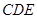 所成角的正弦值.
所成角的正弦值.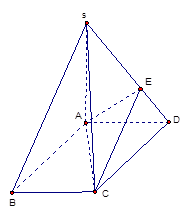
 是边长为1的正方形,
是边长为1的正方形, 分别为
分别为 上的点,且
上的点,且 沿
沿 将正方形折成直二面角
将正方形折成直二面角 .
.
 平面
平面 ;
; 点
点 与平面
与平面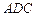 间的距离为
间的距离为 ,试用
,试用 表示
表示