题目内容
【题目】如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=![]() ,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=AD,点M在线段EF上。
,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=AD,点M在线段EF上。

(1)求证:BC⊥平面ACFE;
(2)若![]() ,求证:AM∥平面BDF.
,求证:AM∥平面BDF.
【答案】(1)证明见解析(2)证明见解析
【解析】
(1)由已知梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,易求出AC⊥BC,结合已知中平面ACFE⊥平面ABCD,及平面与平面垂直的性质定理,即可得到BC⊥平面ACFE.
(2)设AC![]() BD=N,则CN:NA=1:2,结合条件可得MF∥AN,且MF=AN,从而得到AM∥NF,由线面平行的判定定理可得结论.
BD=N,则CN:NA=1:2,结合条件可得MF∥AN,且MF=AN,从而得到AM∥NF,由线面平行的判定定理可得结论.
(1)在梯形ABCD中,∵AB∥CD,
AD=CD=CB=a,∠ABC=60°
∴四边形ABCD是等腰梯形
且∠DCA=∠DAC=30°,∠DCB=120°
∴∠ACB=∠DCB-∠DCA=90°
∴AC⊥BC
又∵平面ACFE⊥平面ABCD,交线为AC,
∴BC⊥平面ACFE.
(2)在梯形ABCD中,设AC![]() BD=N,连接FN,则CN:NA=1:2
BD=N,连接FN,则CN:NA=1:2
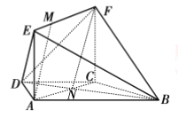
又∵EM:MF=1:2,而EF=AC
∴MF∥AN,且MF=AN
∴四边形ANFM是平行四边形,
∴AM∥NF
又∵NF![]() 平面BDF,AM
平面BDF,AM![]() 平面BDF
平面BDF
∴AM∥平面BDF.

【题目】某品牌经销商在一广场随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有![]() 的把握认为“微信控”与“性别”有关?
的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,再随机抽取3人赠送礼品,试求抽取3人中恰有2人是“微信控”的概率.
参考公式: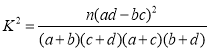 ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.040 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |