题目内容
【题目】已知定义域为![]() 的函数
的函数![]() 是奇函数,其中
是奇函数,其中![]() 为实数.
为实数.
(1)求实数![]() 的值;
的值;
(2)用定义证明![]() 在
在![]() 上是减函数;
上是减函数;
(3)若对于任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;
;![]() (2)证明见解析(3)
(2)证明见解析(3)![]()
【解析】
(1)由![]() 定义域为
定义域为![]() ,且利用奇函数的性质
,且利用奇函数的性质![]() ,再找一组互为相反数代入
,再找一组互为相反数代入![]() 得到另外一个方程,解出
得到另外一个方程,解出![]() 的值;(2)用定义设
的值;(2)用定义设![]() ,然后计算
,然后计算![]() 的正负来判断函数单调性;(3)若
的正负来判断函数单调性;(3)若![]() ,根据
,根据![]() 是单调递减的奇函数,进行移项变形,列出
是单调递减的奇函数,进行移项变形,列出![]() 和
和![]() 的不等式,进而求得实数
的不等式,进而求得实数![]() 的取值范围。
的取值范围。
(1)∵![]() 是
是![]() 上的奇函数,所以
上的奇函数,所以![]() .故
.故![]() ,可得
,可得![]() .
.
又![]() ,解得
,解得![]() .
.
经检验,当![]() 且
且![]() 时,
时,![]() ,满足
,满足![]() 是
是![]() 上的奇函数.
上的奇函数.
(2)由(1)得![]() .任取实数
.任取实数![]() ,且
,且![]() ,
,
则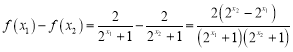 .
.
∵![]() ,∴
,∴![]() ,且
,且![]() ∴
∴![]() ,即
,即![]() ,
,
∴函数![]() 在
在![]() 上是减函数.
上是减函数.
(3)由(1)和(2)知,不等式![]() 恒成立,
恒成立,
即![]() 恒成立,
恒成立,
故![]() 对任意的
对任意的![]() 恒成立,
恒成立,
即![]() 对任意的
对任意的![]() 恒成立.
恒成立.
令![]() ,
,![]() 易知当
易知当![]() 时,
时,![]() 取得最大值8,∴
取得最大值8,∴![]()
故实数![]() 的取值范围是
的取值范围是![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某电动汽车“行车数据”的两次记录如下表:
记录时间 | 累计里程 (单位:公里) | 平均耗电量(单位: | 剩余续航里程 (单位:公里) |
2019年1月1日 | 4000 | 0.125 | 280 |
2019年1月2日 | 4100 | 0.126 | 146 |
(注:累计里程指汽车从出厂开始累计行驶的路程,累计耗电量指汽车从出厂开始累计消耗的电量,平均耗电量=![]() ,剩余续航里程=
,剩余续航里程=![]() ,下面对该车在两次记录时间段内行驶100公里的耗电量估计正确的是
,下面对该车在两次记录时间段内行驶100公里的耗电量估计正确的是
A. 等于12.5B. 12.5到12.6之间
C. 等于12.6D. 大于12.6