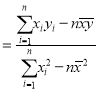Question

【题目】某厂生产某种产品的年固定成本为250万元,每生产千件，需另投入成本为,当年产量不足80千件时,（万元）；当年产量不小于80千件时，（万元）.每件商品售价为0.05万元,通过市场分析,该厂生产的商品能全部销售完.

(1)写出年利润（万元）关于年产量（千件）的函数解析式；

(2)年产量为多少千件时，该厂在这一产品的生产中所获利润最大，最大利润是多少？

Answer 1

【答案】(1)；(2)年产量为100千件时，该厂在这一商品的生产中所获利润最大为1000万元．

【解析】

(1)根据题意可以分成两种情况进行分析讨论：一是当时,二是当时，根据年利润=销售收入-成本,这样可以用分段函数形式写出年利润（万元）关于年产量（千件）的函数解析式；

(2)分别利用配方法和基本不等式求出当时、当时,函数的最大值,通过比较,最后求出函数的最大值.

(1)∵每件商品售价为0.05万元,∴千件商品销售额为万元,

①当时,根据年利润=销售收入-成本,

∴；

②当时,根据年利润=销售收入-成本,

∴.

综①②可得,；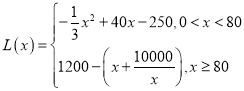

(2)①当时,,

∴当时，取得最大值万元；

②当时,,当且仅当,即时,取得最大值万元．

综合①②,由于,∴年产量为100千件时,该厂在这一商品的生产中所获利润最大为1000万元．