题目内容
设a为实常数,函数y=2x2+(x-a)|x-a|.
(1)当x=0时,y≥1,试求实数a的取值范围.
(2)当a=1时,求y在x≥a时的最小值;当a∈R时,试写出y的最小值(不必写出解答过程).
(3)当x∈(a,+∞)时,求不等式y≥1的解集.
(1)当x=0时,y≥1,试求实数a的取值范围.
(2)当a=1时,求y在x≥a时的最小值;当a∈R时,试写出y的最小值(不必写出解答过程).
(3)当x∈(a,+∞)时,求不等式y≥1的解集.
(1)因为当x=0时,y≥1,故,-a|a|≥1⇒
⇒a≤-1;
(2)当a=1时,y=3x2-2x+1(x≥1).
函数在[1,+∞)上为增函数,
故y在x≥1的最小值为y=3•12-2•1+1=2;
当a∈R时,
若x≥a,则y=3x2-2ax+a2,ymin=
.
若x≤a,则y=x2+2ax-a2,ymin=
.
综上,当a∈R时,ymin=
;
(3)x∈(a,+∞)时,由y≥1,得3x2-2ax+a2-1≥0,△=4a2-12(a2-1)=12-8a2
当a≤-
或a≥
时,△≤0,x∈(a,+∞);
当-
<a<
时,△>0,得:
,
讨论得:当a∈(
,
)时,解集为(a,+∞);
当a∈(-
,-
)时,
解集为(a,
]∪[
,+∞);
当a∈[-
,
]时,
解集为[
,+∞).
|
(2)当a=1时,y=3x2-2x+1(x≥1).
函数在[1,+∞)上为增函数,
故y在x≥1的最小值为y=3•12-2•1+1=2;
当a∈R时,
若x≥a,则y=3x2-2ax+a2,ymin=
|
若x≤a,则y=x2+2ax-a2,ymin=
|
综上,当a∈R时,ymin=
|
(3)x∈(a,+∞)时,由y≥1,得3x2-2ax+a2-1≥0,△=4a2-12(a2-1)=12-8a2
当a≤-
| ||
| 2 |
| ||
| 2 |
当-
| ||
| 2 |
| ||
| 2 |
|
讨论得:当a∈(
| ||
| 2 |
| ||
| 2 |
当a∈(-
| ||
| 2 |
| ||
| 2 |
解集为(a,
a-
| ||
| 3 |
a+
| ||
| 3 |
当a∈[-
| ||
| 2 |
| ||
| 2 |
解集为[
a+
| ||
| 3 |

练习册系列答案
相关题目
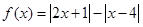 .
.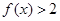 ;
;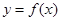 的最小值.
的最小值. .
.