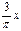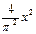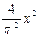题目内容
已知集合A={x|x2+3x+2<0}若B={x|x2-4ax+3a2<0},A⊆B,求实数a的取值范围.
A={x|x2+3x+2<0}={x|-2<x<-1},B={x|x2-4ax+3a2<0}={x|(x-a)(x-3a)<0},
①当3a>a,即a>0时,则B={x|a<x<3a},此时A⊆B不成立;
②当3a=a,即a=0时,则B=ϕ,此时A⊆B不成立;
③当3a<a,即a<0,则B={x|3a<x<a},
∵A⊆B,
∴
?-1≤a≤-
,
故实数a的取值范围为[-1,-
].
综合①②③可得,实数a的取值范围是[-1,-
].
①当3a>a,即a>0时,则B={x|a<x<3a},此时A⊆B不成立;
②当3a=a,即a=0时,则B=ϕ,此时A⊆B不成立;
③当3a<a,即a<0,则B={x|3a<x<a},
∵A⊆B,
∴
|
| 2 |
| 3 |
故实数a的取值范围为[-1,-
| 2 |
| 3 |
综合①②③可得,实数a的取值范围是[-1,-
| 2 |
| 3 |

练习册系列答案
相关题目
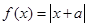 .
.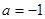 时,求不等式
时,求不等式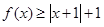 的解集;
的解集;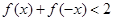 存在实数解,求实数
存在实数解,求实数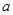 的取值范围.
的取值范围. .
.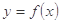 的导函数为
的导函数为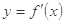 ,且
,且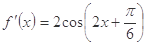 ,则
,则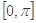 上的单调增区间为( )
上的单调增区间为( )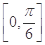
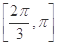
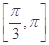
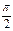 ,则下列命题中正确的是
,则下列命题中正确的是