题目内容
5.将函数y=sin2x的图象向左平移φ(0<φ<π)个单位后得函数$y=sin({2x-\frac{π}{3}})$的图象,则φ的值为( )| A. | $\frac{π}{3}$ | B. | $\frac{5π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{6}$ |
分析 根据y=Asin(ωx+φ)的图象变换规律,变换后得到的是函数y=sin(2x+2φ) 的图象,而已知得到的是函数$y=sin({2x-\frac{π}{3}})$的图象,可得2φ=$\frac{5π}{3}$,由此求得φ的值.
解答 解:将函数y=sin2x的图象向左平移φ(0≤φ<π)个单位后,得函数y=sin2(x+φ)=sin(2x+2φ) 的图象,
而已知得到的是函数$y=sin({2x-\frac{π}{3}})$=sin(2x+$\frac{5π}{3}$)的图象.
结合0≤φ<π可得 2φ=$\frac{5π}{3}$,解得φ=$\frac{5π}{6}$,
故选:B.
点评 本题主要考查诱导公式的应用,利用了y=Asin(ωx+φ)的图象变换规律,属于中档题.

练习册系列答案
相关题目
13.函数y=x4(2-x2)(0<x<$\sqrt{2}$)的最大值是( )
| A. | 0 | B. | 1 | C. | $\frac{16}{27}$ | D. | $\frac{32}{27}$ |
14.已知α,β∈($\frac{3π}{2}$,2π),满足tan(α+β)-2tanβ=0,则tanα的最小值是( )
| A. | $\frac{{3\sqrt{2}}}{4}$ | B. | -$\frac{{\sqrt{2}}}{4}$ | C. | -$\frac{{3\sqrt{2}}}{4}$ | D. | $\frac{{\sqrt{2}}}{4}$ |
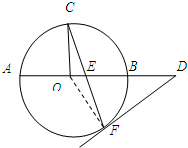 如图,AB是⊙O的直径,C,F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D.连结CF交AB于点E,OA=3,DB=3,则DE=3$\sqrt{3}$.
如图,AB是⊙O的直径,C,F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D.连结CF交AB于点E,OA=3,DB=3,则DE=3$\sqrt{3}$.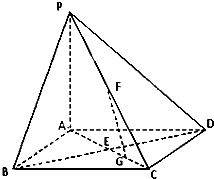 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.