题目内容
(本小题满分13分)
已知定点 ,
, ,动点A满足|AE|=4,线段AF的垂直平分线交AE于点M。
,动点A满足|AE|=4,线段AF的垂直平分线交AE于点M。
(1)求点M的轨迹C1的方程;
(2)抛物线C2: 与C1在第一象限交于点P,直线PF交抛物线于另一个点Q,求抛物线的POQ弧上的点R到直线PQ的距离的最大值。
与C1在第一象限交于点P,直线PF交抛物线于另一个点Q,求抛物线的POQ弧上的点R到直线PQ的距离的最大值。

已知定点
 ,
, ,动点A满足|AE|=4,线段AF的垂直平分线交AE于点M。
,动点A满足|AE|=4,线段AF的垂直平分线交AE于点M。(1)求点M的轨迹C1的方程;
(2)抛物线C2:
 与C1在第一象限交于点P,直线PF交抛物线于另一个点Q,求抛物线的POQ弧上的点R到直线PQ的距离的最大值。
与C1在第一象限交于点P,直线PF交抛物线于另一个点Q,求抛物线的POQ弧上的点R到直线PQ的距离的最大值。
1)依题意有 |ME|+|MF|=|ME|+|MA|
 =|AE|=4>|EF|=2
=|AE|=4>|EF|=2
∴点M的轨迹是以E,F为焦点的椭圆。……3分
∵ ∴
∴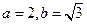 ,
,
故所求点M的轨迹方程是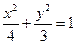 ………6分
………6分
(2)联立方程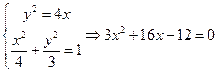
解得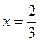 或
或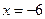 (舍去)
(舍去)
将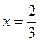 代入抛物线方程得
代入抛物线方程得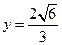 ∴点P的坐标为
∴点P的坐标为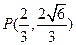 ……8分
……8分
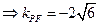 ,于是可得PQ所在直线的方程为:
,于是可得PQ所在直线的方程为: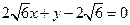 …9分
…9分
设PQ的平行线方程为: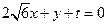
由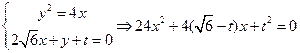
令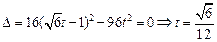 ………………………………………11分
………………………………………11分
∵R到PQ的最大距离即为直线 与PQ之间的距离,故所求为
与PQ之间的距离,故所求为
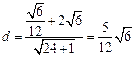 ……………………………………………………13分
……………………………………………………13分
 =|AE|=4>|EF|=2
=|AE|=4>|EF|=2∴点M的轨迹是以E,F为焦点的椭圆。……3分
∵
 ∴
∴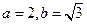 ,
,故所求点M的轨迹方程是
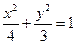 ………6分
………6分(2)联立方程
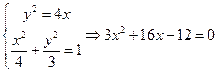
解得
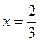 或
或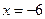 (舍去)
(舍去)将
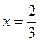 代入抛物线方程得
代入抛物线方程得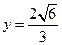 ∴点P的坐标为
∴点P的坐标为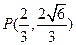 ……8分
……8分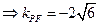 ,于是可得PQ所在直线的方程为:
,于是可得PQ所在直线的方程为: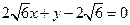 …9分
…9分设PQ的平行线方程为:
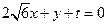
由
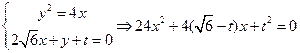
令
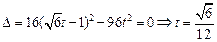 ………………………………………11分
………………………………………11分∵R到PQ的最大距离即为直线
 与PQ之间的距离,故所求为
与PQ之间的距离,故所求为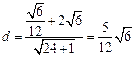 ……………………………………………………13分
……………………………………………………13分略

练习册系列答案
相关题目
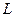 :
: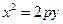 和点
和点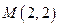 ,若抛物线
,若抛物线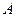 、
、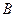 满足
满足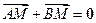 .
.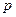 的取值范围;
的取值范围;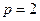 时,抛物线
时,抛物线 ,使得经过
,使得经过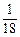 x2-
x2-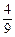 x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)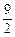 )时,△PQF的面积是否总为定值?若是,求出此定值;若不是,请说明理由;
)时,△PQF的面积是否总为定值?若是,求出此定值;若不是,请说明理由;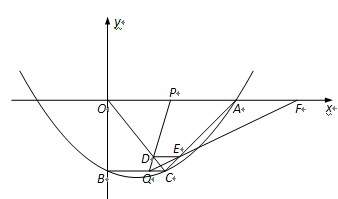
 是抛物线
是抛物线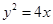 上一动点,则点
上一动点,则点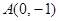 的距离与到直线
的距离与到直线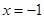 的距离和的最小值是
的距离和的最小值是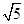
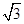
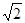
 轴上的抛物线与直线
轴上的抛物线与直线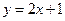 交于P、Q两点,|PQ|=
交于P、Q两点,|PQ|=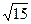 ,求抛物线的方程
,求抛物线的方程
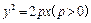 上一点
上一点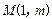 到其焦点的距离为
到其焦点的距离为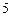 ,双曲线
,双曲线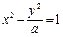 的左顶点为
的左顶点为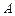 ,若双曲线一条渐近线与直线
,若双曲线一条渐近线与直线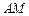 垂直,则实数
垂直,则实数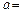 ( )
( )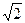
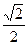

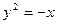 与直线
与直线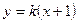 相交于
相交于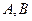 两点。
两点。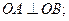
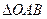 的面积等于
的面积等于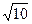 时,求
时,求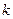 的值。
的值。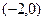 ,则抛物线的标准方程是 .
,则抛物线的标准方程是 . 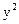 =–x与直线y="k(x" + 1)相交于A、B两点,则△AOB的形状是
=–x与直线y="k(x" + 1)相交于A、B两点,则△AOB的形状是