题目内容
(本小题满分14分)
已知抛物线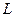 :
: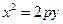 和点
和点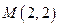 ,若抛物线
,若抛物线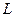 上存在不同两点
上存在不同两点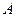 、
、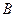 满足
满足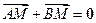 .
.
(1)求实数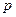 的取值范围;
的取值范围;
(2)当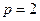 时,抛物线
时,抛物线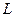 上是否存在异于
上是否存在异于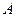 、
、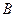 的点
的点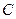 ,使得经过
,使得经过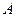 、
、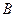 、
、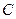 三点的圆和抛物线
三点的圆和抛物线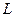 在点
在点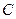 处有相同的切线,若存在,求出点
处有相同的切线,若存在,求出点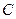 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
已知抛物线
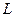 :
: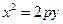 和点
和点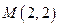 ,若抛物线
,若抛物线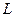 上存在不同两点
上存在不同两点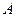 、
、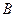 满足
满足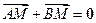 .
.(1)求实数
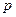 的取值范围;
的取值范围;(2)当
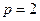 时,抛物线
时,抛物线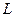 上是否存在异于
上是否存在异于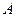 、
、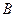 的点
的点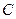 ,使得经过
,使得经过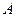 、
、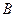 、
、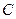 三点的圆和抛物线
三点的圆和抛物线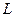 在点
在点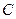 处有相同的切线,若存在,求出点
处有相同的切线,若存在,求出点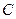 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.解法1:(1)不妨设A
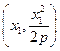 ,B
,B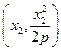 ,且
,且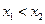 ,
,∵
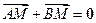 ,∴
,∴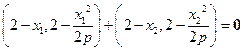 .
.∴
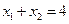 ,
,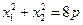 .…………………4分
.…………………4分∵
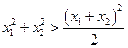 (
(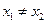 ),即
),即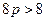 ,
,∴
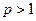 ,即
,即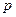 的取值范围为
的取值范围为 .…………………6分
.…………………6分(2)当
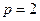 时,由(1)求得
时,由(1)求得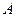 .
.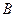 的坐标分别为
的坐标分别为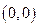 .
.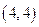 .
.假设抛物线
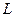 上存在点
上存在点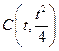 (
(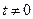 且
且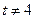 ),…………8分
),…………8分使得经过
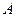 .
.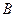 .
.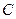 三点的圆和抛物线
三点的圆和抛物线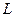 在点
在点
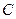 处有相同的切线.
处有相同的切线.设经过
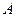 .
.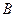 .
.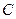 三点的圆的方程为
三点的圆的方程为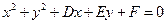 ,
,则
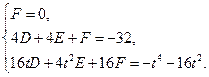
整理得
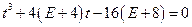 . ①…………9分
. ①…………9分∵函数
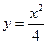 的导数为
的导数为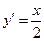 ,
,∴抛物线
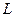 在点
在点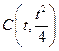 处的切线的斜率为
处的切线的斜率为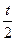 ,
,∴经过
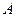 .
.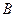 .
.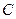 三点的圆
三点的圆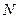 在点
在点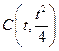 处的切线
处的切线斜率为
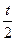 .………10分
.………10分∵
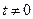 ,∴直线
,∴直线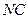 的斜率存在.
的斜率存在.∵圆心
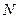 的坐标为
的坐标为 ,
,∴
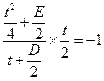 ,
,即
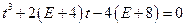 . ②…………………12分
. ②…………………12分∵
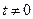 ,由①.②消去
,由①.②消去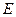 ,得
,得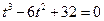 .
.即
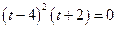 .
.∵
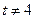 ,∴
,∴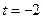 .
.故满足题设的点
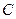 存在,其坐标为
存在,其坐标为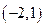 .…………………14分
.…………………14分解法2:(1)设
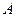 ,
,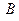 两点的坐标为
两点的坐标为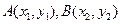
 ,且
,且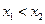 。
。∵
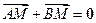 ,可得
,可得 为
为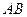 的中点,
的中点,即
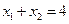 .…………………2分
.…………………2分显然直线
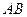 与
与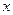 轴不垂直,
轴不垂直,设直线
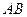 的方程为
的方程为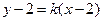 ,
,即
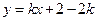 ,…………………3分
,…………………3分将
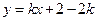 代入
代入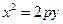 中,
中,得
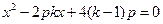 . …………………4分
. …………………4分∴
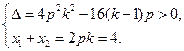 ∴
∴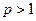 .
.故
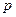 的取值范围为
的取值范围为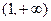 . …………………6分
. …………………6分(2)当
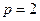 时,由(1)求得
时,由(1)求得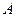 ,
,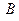 的坐标分别为
的坐标分别为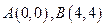 .
. 假设抛物线
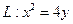 上存在点
上存在点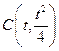 (
(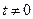 且
且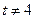 ),
),使得经过
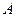 .
.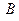 .
.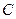 三点的圆和抛物线
三点的圆和抛物线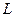 在点
在点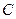 处有相同的切线.
处有相同的切线.设圆的圆心坐标为
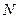
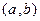 ,
,∵
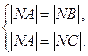
∴
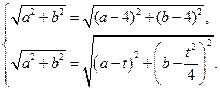
即
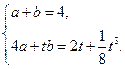 …………………8分
…………………8分解得
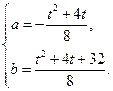 …………………10分
…………………10分∵抛物线
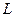 在点
在点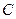 处切线的斜率为
处切线的斜率为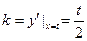 ,
,而
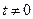 ,且该切线与
,且该切线与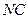 垂直,∴
垂直,∴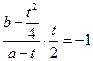 .
. 即
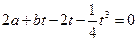 .…………………12分
.…………………12分将
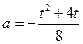 ,
,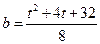 代入上式,
代入上式,得
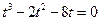 .
.即
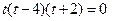
∵
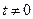 且
且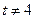 ,∴
,∴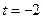 .
.故满足题设的点
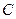 存在,其坐标为
存在,其坐标为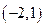 . …………………14分
. …………………14分略

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
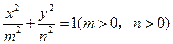 的右焦点与抛物线
的右焦点与抛物线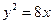 的焦点相同,离心率为
的焦点相同,离心率为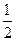 ,则此椭圆的方程为( )
,则此椭圆的方程为( )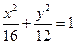
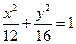
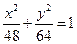
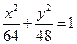
 ,
, ,动点A满足|AE|=4,线段AF的垂直平分线交AE于点M。
,动点A满足|AE|=4,线段AF的垂直平分线交AE于点M。 与C1在第一象限交于点P,直线PF交抛物线于另一个点Q,求抛物线的POQ弧上的点R到直线PQ的距离的最大值。
与C1在第一象限交于点P,直线PF交抛物线于另一个点Q,求抛物线的POQ弧上的点R到直线PQ的距离的最大值。
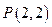 为
为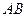 的中点,则抛物线C的方程为
的中点,则抛物线C的方程为 
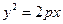 上,横坐标为4的点到焦点的距离为5,则
上,横坐标为4的点到焦点的距离为5,则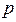 的值为( )
的值为( )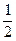 B 1 C 2 D 4
B 1 C 2 D 4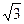 ,则M到该抛物线焦点的距离为
,则M到该抛物线焦点的距离为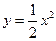 (
(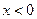 )上,并且与抛物线的准线及y轴都相切的圆的方程是_
)上,并且与抛物线的准线及y轴都相切的圆的方程是_