题目内容
(本题满分14分)
已知函数 ,
, ,
,
(Ⅰ)当 时,若
时,若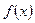 在
在 上单调递增,求
上单调递增,求 的取值范围;
的取值范围;
(Ⅱ)求满足下列条件的所有实数对 :当
:当 是整数时,存在
是整数时,存在 ,使得
,使得 是
是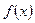 的最大值,
的最大值, 是
是 的最小值;
的最小值;
(Ⅲ)对满足(Ⅱ)的条件的一个实数对 ,试构造一个定义在
,试构造一个定义在 ,且
,且 上的函数
上的函数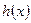 ,使当
,使当 时,
时,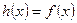 ,当
,当 时,
时,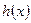 取得最大值的自变量的值构成以
取得最大值的自变量的值构成以 为首项的等差数列。
为首项的等差数列。
解:(Ⅰ)当 时,
时,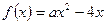 ,
,
若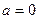 ,
,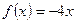 ,则
,则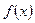 在
在 上单调递减,不符题意。
上单调递减,不符题意。
故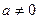 ,要使
,要使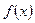 在
在 上单调递增,必须满足
上单调递增,必须满足 ,
,
∴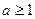 。 (4分)
。 (4分)
(Ⅱ)若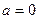 ,
,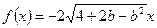 ,则
,则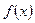 无最大值,故
无最大值,故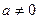 ,
,
∴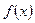 为二次函数,
为二次函数,
要使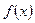 有最大值,必须满足
有最大值,必须满足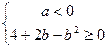 ,即
,即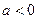 且
且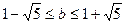 ,
,
此时,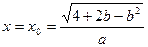 时,
时,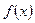 有最大值。
有最大值。
又 取最小值时,
取最小值时,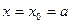 ,依题意,有
,依题意,有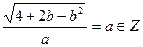 ,
,
则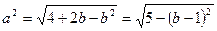 ,
,
∵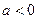 且
且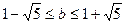 ,∴
,∴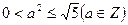 ,得
,得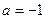 ,此时
,此时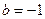 或
或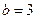 。
。
∴满足条件的实数对 是
是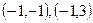 。 (9分)
。 (9分) 
(Ⅲ)当实数对 是
是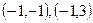 时,
时,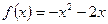 (14分)
(14分)
依题意,只需构造以2(或2的正整数倍)为周期的周期函数即可。
如对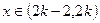 ,
,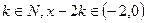 ,
,
此时,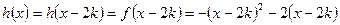 ,
,
故
解析

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 (
( )
)  的单调递减区间;
的单调递减区间;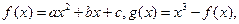 (
(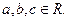 )若
)若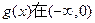 上是增函数,在(0,1)上是减函数,函数
上是增函数,在(0,1)上是减函数,函数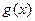 在R上有三个零点,且1是其中一个零点。
在R上有三个零点,且1是其中一个零点。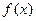 最小值的取值范围。
最小值的取值范围。
 时,求函数
时,求函数 的单调区间;
的单调区间; 的图像在点
的图像在点 处的切线的倾斜角为
处的切线的倾斜角为 ,问:
,问: 在什么范围取值时,函数
在什么范围取值时,函数 在区间
在区间 上总存在极值?
上总存在极值?
 的单调减区间;
的单调减区间; 满足,
满足, 求证:
求证: ;
; ,
, 为数列
为数列 的前
的前 项和,求证:
项和,求证: 。
。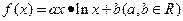 ,在点
,在点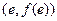 处的切
处的切 线方程是
线方程是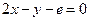 (e为自然对数的底)。
(e为自然对数的底)。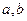 的值及
的值及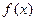 的解析式;
的解析式;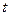 是正数,设
是正数,设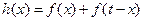 ,求
,求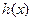 的最小值;
的最小值; 于x的不等式
于x的不等式 对一切
对一切 恒成立,求实数
恒成立,求实数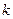 的取值范围
的取值范围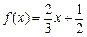 ,
,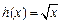 .
.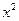 [h(x)]
[h(x)]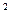 ,求F(x)的单调区间与极值;
,求F(x)的单调区间与极值;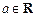 ,解关于x的方程
,解关于x的方程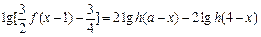 ;
;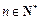 ,证明:
,证明: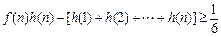 .
. (吨)与每吨产品的价格p(元/吨)之间的关系式为:p=24200-0.2x2,且生产x吨的成本为
(吨)与每吨产品的价格p(元/吨)之间的关系式为:p=24200-0.2x2,且生产x吨的成本为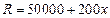 (元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(注:利润=收入─成本)
(元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(注:利润=收入─成本)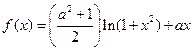

 .
.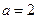 时,求
时,求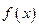 的极值
的极值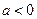 时,讨论
时,讨论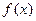 的单调性。
的单调性。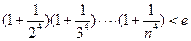 (
(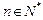 ,
,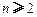 ,其中无理数
,其中无理数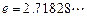 )
)