Question

【题目】已知点在曲线上，⊙过原点，且与轴的另一个交点为，若线段，⊙和曲线上分别存在点、点和点，使得四边形（点， ， ， 顺时针排列）是正方形，则称点为曲线的“完美点”．那么下列结论中正确的是（ ）．

A. 曲线上不存在”完美点”

B. 曲线上只存在一个“完美点”，其横坐标大于

C. 曲线上只存在一个“完美点”，其横坐标大于且小于

D. 曲线上存在两个“完美点”，其横坐标均大于

Answer 1

【答案】B

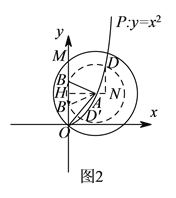
【解析】如图，如果点为“完美点”则有，以为圆心， 为半径作圆（如图中虚线圆）交轴于， （可重合），交抛物线于点， 当且仅当时，在圆上总存在点，使得为的角平分线，即，利用余弦定理可求得此时，即四边形是正方形，即点为“完美点”，如图，结合图象可知，点一定是上方的交点，否则在抛物线上不存在使得， 也一定是上方的点，否则， ， ， ， 不是顺时针，再考虑当点横坐标越来越大时， 的变化情况：

设，当时， ，此时圆与轴相离，此时点不是“完美点”，故只需要考虑，当增加时， 越来越小，且趋近于，而当时， ；故曲线上存在唯一一个“完美点”其横坐标大于．故选．