题目内容
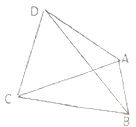
【题目】如图所示,在平面四边形![]() 中,
中, ![]() ,
, ![]() 为正三角形,则
为正三角形,则![]() 面积的最大值为( )
面积的最大值为( )
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】在△ABC中,设∠ACB=α,∠ACB=β,由余弦定理得:
AC2=12+22-2×1×2cosα=5-4cosα,
∵△ACD为正三角形,
∴CD2=5-4cosα,
由正弦定理得: ![]()
∵(CDcosβ)2=CD2(1-sin2β)=CD2-sin2α=5-4cosα-sin2α=(2-cosα)2,
∵β<∠BAC,∴β为锐角,CDcosβ=2-cosα,
∴S△BCD=![]() 2CDsin(
2CDsin(![]() +β)=CDsin(
+β)=CDsin(![]() +β)=
+β)=![]() CDcosβ+
CDcosβ+![]() CDsinβ=
CDsinβ=![]()
(2-cosα)+![]() sinα=
sinα=![]() +sin(α-
+sin(α-![]() )当α=
)当α=![]() 时,(S△BCD)max=
时,(S△BCD)max=![]() +1
+1
故选D

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案【题目】随着我国经济的快速发展,民用汽车的保有量也迅速增长.机动车保有量的发展影响到环境质量、交通安全、道路建设等诸多方面.在我国,尤其是大中型城市,机动车已成为城市空气污染的重要来源.因此,合理预测机动车保有量是未来进行机动车污染防治规划、道路发展规划等的重要前提.从2012年到2016年,根据“云南省某市国民经济和社会发展统计公报”中公布的数据,该市机动车保有量数据如表所示.
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
机动车保有量 | 169 | 181 | 196 | 215 | 230 |
(1)在图所给的坐标系中作出数据对应的散点图;
(2)建立机动车保有量![]() 关于年份代码
关于年份代码![]() 的回归方程;
的回归方程;
(3)按照当前的变化趋势,预测2017年该市机动车保有量.
附注:回归直线方程![]() 中的斜率和截距的最小二乘估计公式分别为:
中的斜率和截距的最小二乘估计公式分别为:
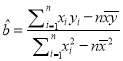 ,
, ![]() .
.
【题目】甲、乙两家外卖公司,其送餐员的日工资方案如下:甲公司的底薪80元,每单抽成4元;乙公司无底薪,40单以内(含40单)的部分每单抽成6元,超出40单的部分每单抽成7元,假设同一公司送餐员一天的送餐单数相同,现从两家公司各随机抽取一名送餐员,并分别记录其50天的送餐单数,得到如下频数表:
甲公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 10 | 15 | 10 | 10 | 5 |
乙公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 5 | 10 | 10 | 20 | 5 |
(1)现从甲公司记录的50天中随机抽取3天,求这3天送餐单数都不小于40的概率;
(2)若将频率视为概率,回答下列两个问题:
①记乙公司送餐员日工资为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②小王打算到甲、乙两家公司中的一家应聘送餐员,如果仅从日工资的角度考虑,请利用所学的统计学知识为小王作出选择,并说明理由.