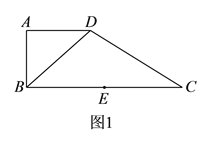
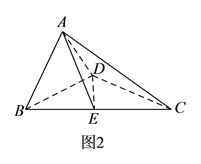
题目内容
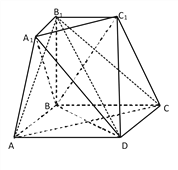
【题目】如图所示的几何体是由棱台![]() 和棱锥
和棱锥![]() 拼接而成的组合体,其底面四边形
拼接而成的组合体,其底面四边形![]() 是边长为
是边长为![]() 的菱形,且
的菱形,且![]() ,
, ![]()
![]() 平面
平面![]() ,
, ![]() .
.
(1)求证:平面![]()
![]() 平面
平面![]()
![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() ;
;
【解析】试题分析:
(1)要证明平面![]() ⊥平面
⊥平面![]() ,由面面垂直的判定定理知,需在某个平面上找到某条直线垂直于另一个平面,通过观察分析,平面
,由面面垂直的判定定理知,需在某个平面上找到某条直线垂直于另一个平面,通过观察分析,平面![]() 内直线
内直线![]() 平面
平面![]() .要证明
.要证明![]() 平面
平面![]() ,又转化为线面垂直问题,
,又转化为线面垂直问题, ![]() ⊥平面
⊥平面![]() ∴
∴![]() ⊥
⊥![]() ,菱形
,菱形![]() 中,
中, ![]() ⊥
⊥![]() ,又
,又![]() ∴
∴![]() 平面
平面![]() .
.
(2)建立空间直角坐标系,分别求出平面![]() 平面DFC的法向量,再求出两个法向量的夹角的余弦值,即可得二面角
平面DFC的法向量,再求出两个法向量的夹角的余弦值,即可得二面角![]() 的余弦值.
的余弦值.
试题解析:
(1)∵![]() ⊥平面
⊥平面![]() ∴
∴![]() ⊥
⊥![]()
在菱形![]() 中,
中, ![]() ⊥
⊥![]()
又![]() ∴
∴![]() 平面
平面![]()
∵![]() 平面
平面![]() ∴平面
∴平面![]() ⊥平面
⊥平面![]()

(2)连接![]() 、
、![]() 交于点
交于点![]() ,以
,以![]() 为坐标原点,以
为坐标原点,以![]() 为
为![]() 轴,以
轴,以![]() 为
为![]() 轴,如图建立空间直角坐标系.
轴,如图建立空间直角坐标系. ![]()
 ,同理
,同理
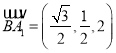 ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]()
![]()
![]() ,则
,则![]()
设平面DFC的法向量![]()
 ,则
,则![]()
设二面角![]() 为
为![]() ,
, 

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:
(Ⅰ)在4月份任取一天,估计西安市在该天不下雨的概率;
(Ⅱ)西安市某学校拟从4月份的一个晴天开始举行连续2天的运动会,估计运动会期间不下雨的概率.
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
天气 | 晴 | 雨 | 阴 | 阴 | 阴 | 雨 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 晴 |
日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
天气 | 晴 | 阴 | 雨 | 阴 | 阴 | 晴 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 雨 |