题目内容
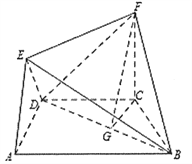
【题目】在如图所示的几何体中,四边形![]() 是等腰梯形,
是等腰梯形, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.

【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:(1)由题意及图可得,先由条件证得![]() ,再根据
,再根据![]() ,再由线面垂直的判定定理即可证得线面垂直;(2)解法一:由(1)知,
,再由线面垂直的判定定理即可证得线面垂直;(2)解法一:由(1)知, ![]() ,可得出
,可得出![]() ,结合
,结合![]() 平面
平面![]() ,知
,知![]() 两两垂直,因此可以
两两垂直,因此可以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
, ![]() ,
, ![]() 所在的直线为
所在的直线为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立空间直角坐标系,不妨设
轴建立空间直角坐标系,不妨设![]() ,表示出各点的坐标,再求出两个平面的法向量的坐标,即可由公式求出二面角
,表示出各点的坐标,再求出两个平面的法向量的坐标,即可由公式求出二面角![]() 的余弦值;解法二:取
的余弦值;解法二:取![]() 的中点
的中点![]() ,连接
,连接![]() ,由于
,由于![]() ,因此
,因此![]() ,又
,又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,可证明出
,可证明出![]() 为二面角
为二面角![]() 的平面角,再解三角形即可求出二面角
的平面角,再解三角形即可求出二面角![]() 的余弦值.
的余弦值.
试题解析:(1)因为四边形![]() 是等腰梯形,
是等腰梯形, ![]() ,
,
![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() ,
,
因此![]() ,
, ![]() ,
,
又![]() ,且
,且![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)解法一:由(1)知![]() ,所以
,所以![]()
又![]() 平面
平面![]() ,因此
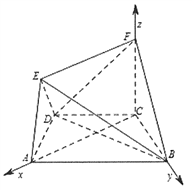
,因此![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
, ![]() ,
, ![]() 所在的直线为
所在的直线为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴,建立如图所示的空间直角坐标系.不妨设
轴,建立如图所示的空间直角坐标系.不妨设![]() ,则
,则![]() ,
, ![]() ,
, 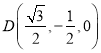 ,
, ![]()
因此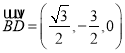 ,
, ![]()
设平面![]() 的法向量为
的法向量为![]()
由于![]() ,取
,取![]() ,则
,则![]() ,
,
由于![]() 是平面
是平面![]() 的一个法向量,则
的一个法向量,则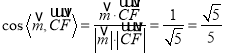
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
解法二:如图,取![]() 的中点
的中点![]() ,连接
,连接![]()
由于![]() ,因此
,因此![]() ,
,
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() ,
,
由于![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,故
,故![]() ,所以
,所以![]() 为二面角
为二面角![]() 的平面角
的平面角
在等腰三角形![]() 中,由于
中,由于![]() ,
,
因此![]() ,
,
又![]() ,所以
,所以![]() ,
,
故![]() ,因此二面角
,因此二面角![]() 的余弦值为
的余弦值为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某大型娱乐场有两种型号的水上摩托,管理人员为了了解水上摩托的使用及给娱乐城带来的经济收入情况,对该场所最近6年水上摩托的使用情况进行了统计,得到相关数据如表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
使用率 | 11 | 13 | 16 | 15 | 20 | 21 |
(1)请根据以上数据,用最小二乘法求水上摩托使用率![]() 关于年份代码
关于年份代码![]() 的线性回归方程,并预测该娱乐场2018年水上摩托的使用率;
的线性回归方程,并预测该娱乐场2018年水上摩托的使用率;
(2)随着生活水平的提高,外出旅游的老百姓越来越多,该娱乐场根据自身的发展需要,准备重新购进一批水上摩托,其型号主要是目前使用的Ⅰ型、Ⅱ型两种,每辆价格分别为1万元、1.2万元.根据以往经验,每辆水上摩托的使用年限不超过四年.娱乐场管理部对已经淘汰的两款水上摩托的使用情况分别抽取了50辆进行统计,使用年限如条形图所示:
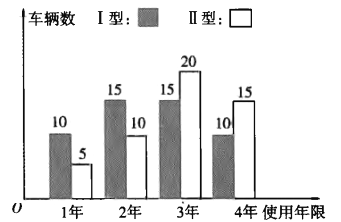
已知每辆水上摩托从购入到淘汰平均年收益是0.8万元,若用频率作为概率,以每辆水上摩托纯利润(纯利润![]() 收益
收益![]() 购车成本)的期望值为参考值,则该娱乐场的负责人应该选购Ⅰ型水上摩托还是Ⅱ型水上摩托?
购车成本)的期望值为参考值,则该娱乐场的负责人应该选购Ⅰ型水上摩托还是Ⅱ型水上摩托?
附:回归直线方程为![]() ,其中
,其中 ,
, ![]() .
.

