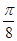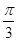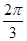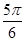题目内容
已知矩阵M=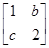 有特征值λ1=4及对应的一个特征向量e1=
有特征值λ1=4及对应的一个特征向量e1=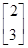 .求:
.求:
(1)矩阵M;
(2)曲线5x2+8xy+4y2=1在M的作用下的新曲线方程.
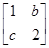 有特征值λ1=4及对应的一个特征向量e1=
有特征值λ1=4及对应的一个特征向量e1=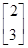 .求:
.求:(1)矩阵M;
(2)曲线5x2+8xy+4y2=1在M的作用下的新曲线方程.
(1)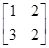 (2)x2+y2=2
(2)x2+y2=2
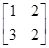 (2)x2+y2=2
(2)x2+y2=2(1)由已知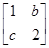
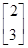 =4
=4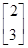 ,
,
则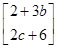 =
=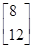 ,即
,即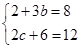 ,得
,得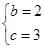 ,所以M=
,所以M=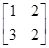 .
.
(2)设曲线上任一点P(x,y),点P在M作用下对应点P′(x′,y′),则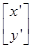 =
=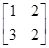
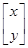 .即
.即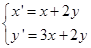 解得
解得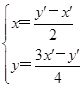 ,
,
代入5x2+8xy+4y2=1,得x′2+y′2=2,
即曲线5x2+8xy+4y2=1在M的作用下的新曲线的方程是x2+y2=2.
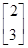 =4
=4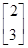 ,
,则
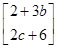 =
=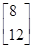 ,即
,即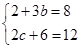 ,得
,得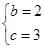 ,所以M=
,所以M=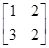 .
.(2)设曲线上任一点P(x,y),点P在M作用下对应点P′(x′,y′),则
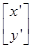 =
=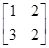
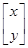 .即
.即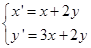 解得
解得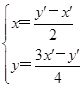 ,
,代入5x2+8xy+4y2=1,得x′2+y′2=2,
即曲线5x2+8xy+4y2=1在M的作用下的新曲线的方程是x2+y2=2.

练习册系列答案
相关题目
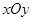 中,直线
中,直线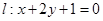 在矩阵
在矩阵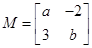 对应的变换作用下得到直线
对应的变换作用下得到直线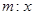
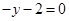 ,求实数
,求实数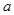 、
、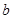 的值.
的值.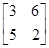 的特征值及相应的特征向量.
的特征值及相应的特征向量.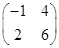 的特征值和特征向量.
的特征值和特征向量.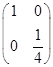 变换作用下的解析式.
变换作用下的解析式.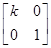 ,N=
,N=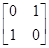 ,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,求k的值.
,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,求k的值.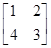 .
.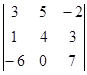 中,元素
中,元素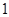 的代数余子式的值是 .
的代数余子式的值是 .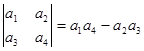 ,将
,将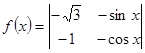 向左平移
向左平移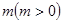 个单位,所得图象对应的函数为偶函数,则
个单位,所得图象对应的函数为偶函数,则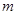 的最小值为( )
的最小值为( )