题目内容
求矩阵M=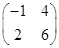 的特征值和特征向量.
的特征值和特征向量.
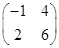 的特征值和特征向量.
的特征值和特征向量.当t≠0时,属于λ1=7的特征向量为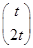
当t≠0时,所以属于λ2=-2的特征向量为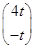
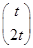
当t≠0时,所以属于λ2=-2的特征向量为
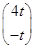
特征多项式λ2-5λ-14=(λ-7)(λ+2),
由(λ-7)(λ+2)=0可得:λ1=7,λ2=-2.
由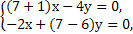 可得2x-y=0,
可得2x-y=0,
∴(x,y)=(t,2t).
当t≠0时,属于λ1=7的特征向量为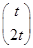 ,
,
由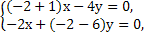 可得x+4y=0,
可得x+4y=0,
∴(x,y)=(4t,-t),
当t≠0时,所以属于λ2=-2的特征向量为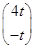 .
.
由(λ-7)(λ+2)=0可得:λ1=7,λ2=-2.
由
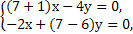 可得2x-y=0,
可得2x-y=0,∴(x,y)=(t,2t).
当t≠0时,属于λ1=7的特征向量为
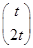 ,
,由
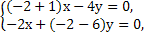 可得x+4y=0,
可得x+4y=0,∴(x,y)=(4t,-t),
当t≠0时,所以属于λ2=-2的特征向量为
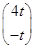 .
.
练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
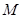 满足:
满足: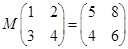 .
.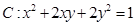 在矩阵
在矩阵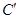 ,求曲线
,求曲线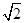 ),求△OAB在矩阵MN的作用下变换所得到的图形的面积,其中矩阵M=
),求△OAB在矩阵MN的作用下变换所得到的图形的面积,其中矩阵M=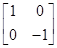 ,N=
,N=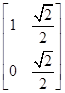 .
.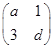 有特征值λ=-1及对应的一个特征向量e1=
有特征值λ=-1及对应的一个特征向量e1=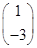 .
.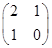 ,求直线x+2y=1在A2对应变换作用下得到的曲线方程.
,求直线x+2y=1在A2对应变换作用下得到的曲线方程.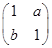 的作用下变换为曲线x2-y2=1,试求a+b的值.
的作用下变换为曲线x2-y2=1,试求a+b的值.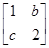 有特征值λ1=4及对应的一个特征向量e1=
有特征值λ1=4及对应的一个特征向量e1=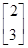 .求:
.求: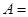
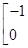
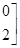 ,
,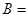
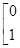
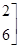 ,求矩阵
,求矩阵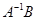 .
.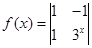 ,则
,则 .
.