题目内容
17.已知p:“函数f(x)为偶函数”是q:“函数g(f(x))为偶函数”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据充分条件和必要条件的定义结合函数奇偶性的性质,进行判断即可.
解答 解:当f(x)为偶函数时,可得g(f(-x))=g(f(x)),故p是q的充分条件;
而当g(f(x))为偶函数时,不能推出“f(x)为偶函数”成立,如g(x)=|x|,f(x)=x3,g(f(x))=|x3|是偶函数,而f(x)不是偶函数,
故选A.
点评 本小题主要借助条件逻辑的判定,考查函数的性质以及对复合函数奇偶性的判定等问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.数列{an}中,an>0,a1=1,an+2=$\frac{1}{{{a_n}+1}}$,若a20=a16,则a2+a3=( )
| A. | $\frac{5}{2}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\frac{{\sqrt{5}-1}}{2}$ | D. | $\frac{{\sqrt{5}+1}}{2}$ |
6.设a,b∈R,则“a>b”是“|a|>|b|”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
7. 如图是一个旋转体的三视图,其中正视图,侧视图都是由半圆和矩形组成,则这个旋转体的体积是( )
如图是一个旋转体的三视图,其中正视图,侧视图都是由半圆和矩形组成,则这个旋转体的体积是( )
 如图是一个旋转体的三视图,其中正视图,侧视图都是由半圆和矩形组成,则这个旋转体的体积是( )
如图是一个旋转体的三视图,其中正视图,侧视图都是由半圆和矩形组成,则这个旋转体的体积是( )| A. | $\frac{8}{3}$π | B. | $\frac{7}{3}$π | C. | 2π | D. | $\frac{5}{3}$π |
 为表示
为表示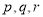 三者中较小的一个, 若函数
三者中较小的一个, 若函数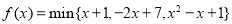 ,则不等式
,则不等式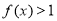 的解集为( )
的解集为( ) B.
B.
 D.
D.
 如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且BN=$\frac{1}{3}$BC
如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且BN=$\frac{1}{3}$BC 如图,在三棱锥A-BCD中,△ACD与△BCD都是边长为2的正三角形,且平面ACD⊥平面BCD,则该三棱锥外接球的表面积为$\frac{20}{3}π$.
如图,在三棱锥A-BCD中,△ACD与△BCD都是边长为2的正三角形,且平面ACD⊥平面BCD,则该三棱锥外接球的表面积为$\frac{20}{3}π$.