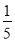题目内容
5. 如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且BN=$\frac{1}{3}$BC
如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且BN=$\frac{1}{3}$BC(1)求证:MN⊥AB
(2)求二面角P-AN-M的余弦值.
分析 (1)以A为原点,AN为x轴的正方向建立如图所示的空间直角坐标系,可得$\overrightarrow{AB}$和$\overrightarrow{MN}$的坐标,证数量积为0即可;
(2)平面PAN的法向量可取为$\overrightarrow{AC}$=(0,1,0),待定系数可得平面AMN的法向量$\overrightarrow{n}$,计算向量的夹角余弦值即可得到二面角P-AN-M的余弦值.
解答  解:(1)由题意可得∠BAN=30°,∴∠NAC=120°-30°=90°,
解:(1)由题意可得∠BAN=30°,∴∠NAC=120°-30°=90°,
以A为原点,AN为x轴的正方向建立如图所示的空间直角坐标系,
可得A(0,0,0),B($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$,0),M($\frac{\sqrt{3}}{4}$,-$\frac{1}{4}$,$\frac{1}{2}$),N($\frac{\sqrt{3}}{3}$,0,0),
∴$\overrightarrow{AB}$=($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$,0),$\overrightarrow{MN}$=($\frac{\sqrt{3}}{12}$,$\frac{1}{4}$,$-\frac{1}{2}$),
∴$\overrightarrow{AB}$•$\overrightarrow{MN}$=0,∴MN⊥AB
(2)由(1)知P(0,0,1),C(0,1,0),
$\overrightarrow{AM}$=($\frac{\sqrt{3}}{4}$,-$\frac{1}{4}$,$\frac{1}{2}$),$\overrightarrow{AN}$=($\frac{\sqrt{3}}{3}$,0,0),
平面PAN的法向量可取为$\overrightarrow{AC}$=(0,1,0),
设平面AMN的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AM}=\frac{\sqrt{3}}{4}x-\frac{1}{4}y+\frac{1}{2}z=0}\\{\overrightarrow{n}•\overrightarrow{AN}=\frac{\sqrt{3}}{3}x=0}\end{array}\right.$,故可取量$\overrightarrow{n}$=(0,2,1),
∴cos<$\overrightarrow{n}$,$\overrightarrow{AC}$>=$\frac{\overrightarrow{n}•\overrightarrow{AC}}{|\overrightarrow{n}||\overrightarrow{AC}|}$=$\frac{2\sqrt{5}}{5}$
∴二面角P-AN-M的余弦值为$\frac{2\sqrt{5}}{5}$
点评 本题考查空间向量法解决立体几何问题,涉及二面角的求解,属中档题.

| x | 1 | 2 | 3 | 4 |
| y | 20 | 30 | 50 | 60 |
(Ⅱ)若用$\frac{y_i}{{{x_i}+3}}$(i=1,2,3,4)表示统计数据的“强化均值”(精确到整数),若“强化均值”的标准差在区间[0,2)内,则强化训练有效,请问这个班的强化训练是否有效?
附:回归直线的斜率和截距的最小二乘法估计公式分别为:$\hat b=\frac{{\sum_{i=1}^n{({x_i}-\bar x)({y_i}-\bar y)}}}{{\sum_{i=1}^n{{{({x_i}-\bar x)}^2}}}}$,$\hat a=\bar y-\hat b\bar x$.
样本数据x1,x2,…,xn的标准差为:s=$\sqrt{\frac{{\sum_{i=1}^n{{{({x_i}-\bar x)}^2}}}}{n}}$.
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | -5 | B. | 1 | C. | 7 | D. | 2 |
 的终边过点
的终边过点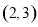 ,则
,则 等于( )
等于( )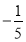 B.
B.