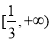题目内容
8.数列{an}中,an>0,a1=1,an+2=$\frac{1}{{{a_n}+1}}$,若a20=a16,则a2+a3=( )| A. | $\frac{5}{2}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\frac{{\sqrt{5}-1}}{2}$ | D. | $\frac{{\sqrt{5}+1}}{2}$ |
分析 由数列递推式求出a3,结合a20=a16求得a16,然后由an+2=$\frac{1}{{{a_n}+1}}$,可得a16=a2,则答案可求.
解答 解:由a1=1,an+2=$\frac{1}{{{a_n}+1}}$,得${a}_{3}=\frac{1}{{a}_{1}+1}=\frac{1}{2}$.
${a}_{20}=\frac{1}{{a}_{18}+1}=\frac{1}{\frac{1}{{a}_{16}+1}+1}={a}_{16}$,
即${{a}_{16}}^{2}+{a}_{16}-1=0$.
∵an>0,∴${a}_{16}=\frac{-1+\sqrt{5}}{2}$.
则由an+2=$\frac{1}{{{a_n}+1}}$及${a}_{16}=\frac{-1+\sqrt{5}}{2}$求得${a}_{2}=\frac{-1+\sqrt{5}}{2}$.
∴a2+a3=$\frac{-1+\sqrt{5}}{2}+\frac{1}{2}=\frac{\sqrt{5}}{2}$.
故选:B.
点评 本题考查了数列递推式,解答此题的关键是对数列规律性的发现,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.设函数$f(x)=\left\{{\begin{array}{l}{ln(-x){,_{\;}}x<0}\\{-lnx,{{,}_{\;}}x>0}\end{array}}\right.$若f(m)>f(-m),则实数m的取值范围是( )
| A. | (-1,0)∪(0,1) | B. | .(-∞,-1)∪(0,1) | C. | (-1,0)∪(1,+∞) | D. | (-1,1] |
13.高考复习经过二轮“见多识广”之后,为了研究考前“限时抢分”强化训练次数x与答题正确率y%的关系,对某校高三某班学生进行了关注统计,得到如下数据:
(Ⅰ)求y关于x的线性回归方程,并预测答题正确率是100%的强化训练次数;
(Ⅱ)若用$\frac{y_i}{{{x_i}+3}}$(i=1,2,3,4)表示统计数据的“强化均值”(精确到整数),若“强化均值”的标准差在区间[0,2)内,则强化训练有效,请问这个班的强化训练是否有效?
附:回归直线的斜率和截距的最小二乘法估计公式分别为:$\hat b=\frac{{\sum_{i=1}^n{({x_i}-\bar x)({y_i}-\bar y)}}}{{\sum_{i=1}^n{{{({x_i}-\bar x)}^2}}}}$,$\hat a=\bar y-\hat b\bar x$.
样本数据x1,x2,…,xn的标准差为:s=$\sqrt{\frac{{\sum_{i=1}^n{{{({x_i}-\bar x)}^2}}}}{n}}$.
| x | 1 | 2 | 3 | 4 |
| y | 20 | 30 | 50 | 60 |
(Ⅱ)若用$\frac{y_i}{{{x_i}+3}}$(i=1,2,3,4)表示统计数据的“强化均值”(精确到整数),若“强化均值”的标准差在区间[0,2)内,则强化训练有效,请问这个班的强化训练是否有效?
附:回归直线的斜率和截距的最小二乘法估计公式分别为:$\hat b=\frac{{\sum_{i=1}^n{({x_i}-\bar x)({y_i}-\bar y)}}}{{\sum_{i=1}^n{{{({x_i}-\bar x)}^2}}}}$,$\hat a=\bar y-\hat b\bar x$.
样本数据x1,x2,…,xn的标准差为:s=$\sqrt{\frac{{\sum_{i=1}^n{{{({x_i}-\bar x)}^2}}}}{n}}$.
17.已知p:“函数f(x)为偶函数”是q:“函数g(f(x))为偶函数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
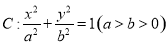 的左、右焦点分别为
的左、右焦点分别为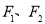 ,椭圆
,椭圆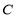 过点
过点 ,直线
,直线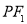 交
交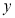 轴于
轴于 ,且
,且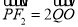 ,
,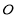 为坐标原点.
为坐标原点. 的方程;
的方程;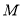 是椭圆
是椭圆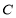 的上顶点,过点
的上顶点,过点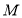 分别作直线
分别作直线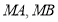 交椭圆
交椭圆 于
于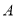 ,
,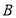 两点,设这两条直线的斜率分别为
两点,设这两条直线的斜率分别为 ,且
,且 ,证明:直线
,证明:直线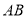 过定点.
过定点. 的定义域为( )
的定义域为( )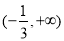 B.
B.
 D.
D.