题目内容
9.已知函数f(x)=sin(2x+$\frac{π}{3}$)与g(x)的图象关于直线x=$\frac{π}{6}$对称,将g(x)的图象向右平移φ(φ>0)个单位后与f(x)的图象重合,则φ的最小值为$\frac{5π}{6}$.分析 函数f(x)=sin(2x+$\frac{π}{3}$)与g(x)的图象关于直线x=$\frac{π}{6}$对称,可得函数g(x)的解析式;再根据函数y=Asin(ωx+φ)的图象变换规律可得sin(2x+$\frac{π}{3}$)=sin(2x-2φ),从而$-2φ=\frac{π}{3}+2kπ$,从而求得φ的最小值.
解答 解:由函数f(x)=sin(2x+$\frac{π}{3}$)与g(x)的图象关于直线x=$\frac{π}{6}$对称,可得函数g(x)的解析式为g(x)=sin2x,
把g(x)的图象向右平移φ个单位后对应解析式为y=f(x)=sin(2x-2φ),
从而$-2φ=\frac{π}{3}+2kπ$,即$φ=-\frac{π}{6}-kπ(k∈Z,k≤-1)$,
∴${φ_{min}}=\frac{5π}{6}$,
故答案为:$\frac{5π}{6}$.
点评 本小题主要考查三角函数的对称,函数y=Asin(ωx+φ)的图象变换规律以及三角函数最值的求取,属于基本试题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
17.已知p:“函数f(x)为偶函数”是q:“函数g(f(x))为偶函数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
4.在△ABC中,角A,B,C的对边分别是a,b,c,若a2-b2=$\sqrt{3}$bc,sinC=2$\sqrt{3}$sinB,则A=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
14.若(x2-$\frac{1}{x}$)5的展开式中含xα(α∈R)的项,则α的值不可能为( )
| A. | -5 | B. | 1 | C. | 7 | D. | 2 |
19.在区间[-3,5]上随机取一个实数a,则使函数f(x)=x2+2ax+4无零点的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
 的定义域为( )
的定义域为( )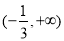 B.
B.
 D.
D.