题目内容
【题目】三棱锥
的三视图如图所示，
.
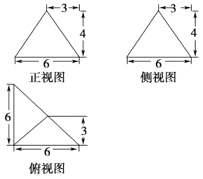
（1）求该三棱锥的表面积；
（2）求该三棱锥内切球的体积.
【答案】（1）
（2）
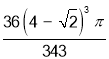
【解析】
（1）根据三视图可知，此三棱锥的底面是腰长为6的等腰直角三角形
，顶点
在底面上的摄影是底面直角三角形斜边的中点，且三棱锥的高为4，要求表面积，再利用三视图，明确
，
，
上的高即可.
（2）根据三棱锥的体积等于以球心为顶点，三棱锥的四个面为底的小三棱锥的体积之和求解.
（1）如图所示：
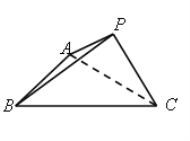
由三视图可知，此三棱锥的底面是腰长为6的等腰直角三角形 ，且
，顶点 在底面上的摄影是底面直角三角形斜边的中点，且三棱锥的高为4，
在
中，边上的高为5，
在
中，边上的高为5，
在
中，边上的高为4，
所以该三棱锥的表面积
（2）设内切球的球心为
，半径为
则由
得
解得
，
所以该三棱锥内切球的体积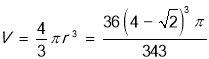
练习册系列答案
相关题目
【题目】越接近高考学生焦虑程度越强，四个高三学生中大约有一个有焦虑症，经有关机构调查，得出距离高考周数与焦虑程度对应的正常值变化情况如下表：
周数x | 6 | 5 | 4 | 3 | 2 | 1 |
正常值y | 55 | 63 | 72 | 80 | 90 | 99 |
(1)作出散点图：
(2)根据上表数据用最小二乘法求出y关于x的线性回归方程 (精确到0.01)；
(3)根据经验，观测值为正常值的0.85～1.06为正常，若1.06～1.12为轻度焦虑，1.12～1.20为中度焦虑，1.20及其以上为重度焦虑，若为中度焦虑及其以上，则要进行心理疏导，若一个学生在距高考第二周时观测值为100，则该学生是否需要进行心理疏导？
（
, 
）
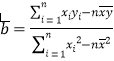