题目内容
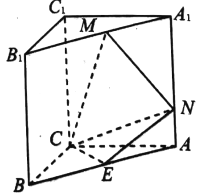
【题目】某亲子公园拟建议广告牌，将边长为
米的正方形ABCD和边长为1米的正方形AEFG在A点处焊接，AM、AN、GM、DN均用加强钢管支撑，其中支撑钢管GM、DN垂直于地面于M点和N点，且GM、DN、MN长度相等
不计焊接点大小
若
时，求焊接点A离地面距离；
若记
，求加强钢管AN最长为多少？
【答案】（1）
米；（2）加强钢管AN最长为3米．
【解析】
（1）
，可用勾股定理求得
，再由直角三角形面积公式求得斜边上的高，从而可得A点到地面的距离；
（2）在
中用余弦定理表示出，设
，由正弦定理用
表示出
，在
中用余弦定理表示出
，并代入，最终把表示为的函数，最后由三角函数的性质可得最值．
当时，
求焊接点A离GD的距离
，
所以：点A离地面的距离为米；
在
中，由于
，
利用余弦定理：
，
所以：
，
设
，
在
中，利用余弦定理：
，
所以：
，
在中，由正弦定理得：
，
所以：
，
代入
式得
，其中
；
所以当
时，
最大，最大值为
；
所以加强钢管AN最长为3米．
练习册系列答案
相关题目
