题目内容
如图,四棱锥P-ABCD的底面为正方形,侧面PAD为等边三角形,且侧面PAD⊥底面ABCD.点M在底面内运动,且满足MP=MC,则点M在正方形ABCD内的轨迹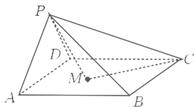
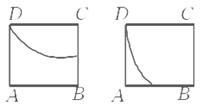
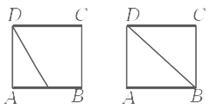
A. B. C. D.
C
解析试题分析:根据题意可知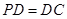 ,则点D符合“M为底面
,则点D符合“M为底面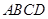 内的一个动点,且满足
内的一个动点,且满足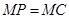 ”
”
设AB的中点为N,根据题目条件可知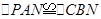 ,∴
,∴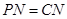 ,点N也符合“M为底面
,点N也符合“M为底面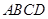 内的一个动点,且满足
内的一个动点,且满足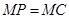 ”,故动点M的轨迹肯定过点D和点N,而到点P与到点N的距离相等的点为线段PC的垂直平分面,线段PC的垂直平分面与平面AC的交线是一直线
”,故动点M的轨迹肯定过点D和点N,而到点P与到点N的距离相等的点为线段PC的垂直平分面,线段PC的垂直平分面与平面AC的交线是一直线
故选C
考点:直线与平面垂直的性质;平面与平面之间的位置关系

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知三条不重合的直线 和两个不重合的平面
和两个不重合的平面 ,下列命题正确的是( )
,下列命题正确的是( )
A.若 , , ,则 ,则 |
B.若 , , ,且 ,且 ,则 ,则 |
C.若 , , ,则 ,则 |
D.若 , , ,且 ,且 ,则 ,则 |
设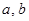 是两条不同直线,
是两条不同直线,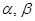 是两个不同平面,下列四个命题中正确的是( )
是两个不同平面,下列四个命题中正确的是( )
A.若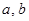 与 与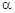 所成的角相等,则 所成的角相等,则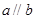 | B.若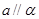 , ,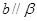 , ,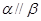 ,则 ,则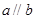 |
C.若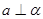 , ,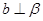 , ,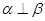 ,则 ,则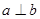 | D.若 , ,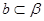 , ,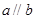 ,则 ,则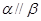 |
如图是正方体的展开图,则在这个正方体中: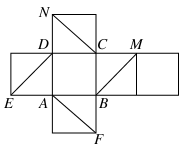
①BM与ED平行;
②CN与BE是异面直线;
③CN与BM成60°角;
④DM与BN垂直.
以上四个命题中,正确命题的序号是( )
| A.①②③ | B.②④ | C.③④ | D.②③④ |
[2012·安徽高考]设平面α与平面β相交于直线m,直线a在平面α内,直线b在平面β内,且b⊥m,则“α⊥β”是“a⊥b”的( )
| A.充分不必要条件 |
| B.必要不充分条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |