题目内容
[2012·安徽高考]设平面α与平面β相交于直线m,直线a在平面α内,直线b在平面β内,且b⊥m,则“α⊥β”是“a⊥b”的( )
| A.充分不必要条件 |
| B.必要不充分条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |
A
解析

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案
相关题目
设m,n是两条不同的直线, ,
, 是两个不同的平面.则下列命题中正确的是( )
是两个不同的平面.则下列命题中正确的是( )
A.m⊥ ,n ,n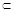  ,m⊥n ,m⊥n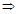  ⊥ ⊥ | B. ⊥ ⊥ , , ∩ ∩ =m,n⊥m =m,n⊥m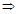 n⊥ n⊥ |
C. ⊥ ⊥ ,m⊥ ,m⊥ ,n∥ ,n∥ 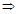 m⊥n m⊥n | D. ∥ ∥ ,m⊥ ,m⊥ ,n∥ ,n∥ 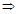 m⊥n m⊥n |
若两条异面直线所成的角为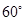 ,则称这对异面直线为“黄金异面直线对”,在连接正方体各顶点的所有直线中,“黄金异面直线对”共有( )
,则称这对异面直线为“黄金异面直线对”,在连接正方体各顶点的所有直线中,“黄金异面直线对”共有( )
| A.12对 | B.18对 | C.24对 | D.30对 |
已知m,n为两条不同的直线, 为两个不同的平面,
为两个不同的平面, ,则下列命题中的假命题是( )
,则下列命题中的假命题是( )
A.若m//n,则 |
B.若 ,则 ,则 |
C.若 相交,则 相交,则 相交 相交 |
D.若 相交,则 相交,则 相交 相交 |
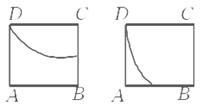
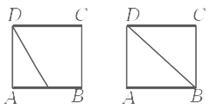
如图中四个正方体图形,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是( )
| A.①③ | B.①④ | C.②③ | D.②④ |
[2013·安徽高考]在下列命题中,不是公理的是( )
| A.平行于同一个平面的两个平面相互平行 |
| B.过不在同一条直线上的三点,有且只有一个平面 |
| C.如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内 |
| D.如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线 |
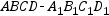 中,M是棱
中,M是棱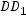 的中点,点O为底面ABCD的中心,P为棱A1B1上任一点,则异面直线OP与AM所成的角的大小为( )
的中点,点O为底面ABCD的中心,P为棱A1B1上任一点,则异面直线OP与AM所成的角的大小为( )