题目内容
在△ABC中,AB=AC=5,BC=6,PA⊥平面ABC,PA=8,则P到BC的距离是( )
A. | B. | C. | D. |
B
解析试题分析:如图:取BC的中点为E,连结AE及PE,由AB=AC=5知: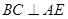 ,又因为PA⊥平面ABC,所以
,又因为PA⊥平面ABC,所以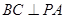 ,从而有
,从而有 ,所以线段PE的长就是P到BC的距离;在
,所以线段PE的长就是P到BC的距离;在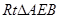 中有AE=4,又PA=8,在
中有AE=4,又PA=8,在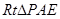 中有
中有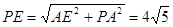 ,故选B.
,故选B.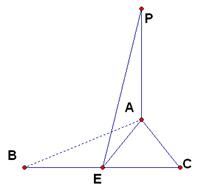
考点:线面的垂直及点到直线的距离.

练习册系列答案
相关题目
设直线 和平面
和平面 ,下列四个命题中,正确的是( )
,下列四个命题中,正确的是( )
A.若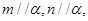 则 则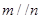 |
B.若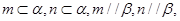 则 则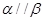 |
C.若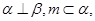 则 则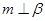 |
D.若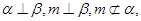 则 则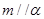 |
已知直二面角 ,点
,点 为垂足,若
为垂足,若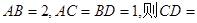 ( )
( )
| A.2 | B.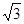 | C. | D.1 |
已知直线 平面
平面 ,直线
,直线
 平面
平面 ,给出下列命题,其中正确的是( )
,给出下列命题,其中正确的是( )
① ②
②
③ ④
④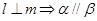
| A.②④ | B.②③④ | C.①③ | D.①②③ |
已知m,n为两条不同的直线, 为两个不同的平面,
为两个不同的平面, ,则下列命题中的假命题是( )
,则下列命题中的假命题是( )
A.若m//n,则 |
B.若 ,则 ,则 |
C.若 相交,则 相交,则 相交 相交 |
D.若 相交,则 相交,则 相交 相交 |
设m、n表示不同直线,α、β表示不同平面,则下列结论中正确的是( )
| A.若m∥α,m∥n,则n∥α |
| B.若m?α,n?β,m∥β,n∥α,则α∥β |
| C.若α∥β,m∥α,m∥n,则n∥β |
| D.若α∥β,m∥α,n∥m,n?β,则n∥β |
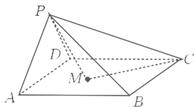
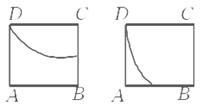
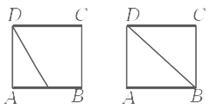
如图中四个正方体图形,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是( )
| A.①③ | B.①④ | C.②③ | D.②④ |

 的扇形,作为圆锥的侧面,求圆锥的表面积和体积.
的扇形,作为圆锥的侧面,求圆锥的表面积和体积.