题目内容
【题目】某企业生产A,B两种产品,生产1吨A种产品需要煤4吨、电18千瓦;生产1吨B种产品需要煤1吨、电15千瓦。现因条件限制,该企业仅有煤10吨,并且供电局只能供电66千瓦,若生产1吨A种产品的利润为10000元;生产1吨B种产品的利润是5000元,试问该企业如何安排生产,才能获得最大利润?
【答案】生产A种产品2吨,B种产品2吨,该企业能够产生最大的利润.
【解析】试题分析:根据已知条件列出约束条件,与目标函数利用线性规划求出最大利润.
试题解析:
设生产A种产品x吨、B种产品y吨,能够产生利润z元,目标函数为![]()
由题意满足以下条件: 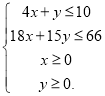
可行域如图
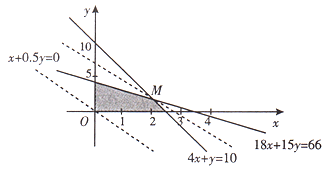
平移直线![]() ,由图可以看出,当直线经过可行域上的点M时,截距最大,即z最大.
,由图可以看出,当直线经过可行域上的点M时,截距最大,即z最大.
解方程组![]() 得M的坐标为x=2,y=2.
得M的坐标为x=2,y=2.
所以zmax=10000x+5000y=30000.
故生产A种产品2吨,B种产品2吨,该企业能够产生最大的利润.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 |
|
|
|
利润 |
|
|
|
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测![]() 月和
月和![]() 月的利润;
月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过![]() 万?
万?
相关公式: 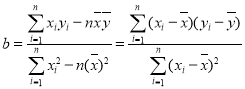 ,
, ![]() .
.